Previous Next

Problem : Given a point in rectangular coordinates (x, y), express it in polar coordinates (r, θ) two different ways such that 0≤θ < 2Π: (x, y) = (1,).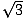

(r, θ) = (2,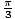),(- 2,).

Problem : Given a point in rectangular coordinates (x, y), express it in polar coordinates (r, θ) two different ways such that 0≤θ < 2Π: (x, y) = (- 4, 0).

(r, θ) = (4, Π),(- 4, 0).

Problem : Given a point in rectangular coordinates (x, y), express it in polar coordinates (r, θ) two different ways such that 0≤θ < 2Π: (x, y) = (- 7, - 7).

(r, θ) = (,),(- ,).

Problem : Given a point in polar coordinates (r, θ), express it in rectangular coordinates (x, y): (r, θ) = (3,).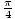

(x, y) = (,).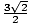

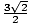Problem : Given a point in polar coordinates (r, θ), express it in rectangular coordinates (x, y): (r, θ) = (1,).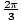

(x, y) = (- ,).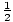

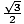Problem : Given a point in polar coordinates (r, θ), express it in rectangular coordinates (x, y): (r, θ) = (0,).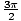

(x, y) = (0, 0).

Problem : How many different ways can a point be expressed in polar coordinates such that r > 0?

An infinite number. (r, θ) = (r, θ +2nΠ), where n is an integer.

Problem : How many different ways can a point be expressed in polar coordinates such that 0≤θ < 2nΠ?

2n. In every cycle of 2Π, there are two pairs of polar coordinates, (r, θ) and (- r, θ + (2n + 1)Π) for every point.
Previous section Next section

Take a Study Break