A sequence is a function whose domain is the positive integers. The value of the function at a given integer is a term of the sequence. The range of a sequence is the set of its terms. Sequences are not typically written as ordered pairs, or drawn as graphs; a sequence is most often represented by a list of its terms starting with the first term, followed by the second, and so on. A general sequence looks something like this: a1, a2, a3,…, an, where n is an integer, and an is the nth term of the sequence. A sequence can also be written as a formula for which any integer can be the input, and the corresponding term is the output.
Here is an example sequence: an = 2n = 2, 4, 6, 8, 10,…, where n is an integer. The formula an = 2n is called an explicit formula for the sequence. By plugging any integer n into the explicit formula for the sequence, the nth term can be found.
Most sequences are defined for all positive integers. They are called infinite sequences. In some cases, though, a sequence may only be defined for the positive integers up to n, a given integer. This might be the case in a sequence that has a real-life application for which integer values above a certain number have no meaning, or are impossible. A sequence defined only for positive integers up to a certain integer are called finite sequences.
When a sequence is given by an explicit formula, it is easy to find the nth term of the sequence. The desired n need only be plugged into the equation to find the nth term. Sometimes, however, a sequence is given by listing the first four or five terms, and then an nth term must be found. In such a case the only way to find the nth term is to study the first few terms and try to find a pattern, and express it in a formula. This is a form of mathematical induction, which is essentially the process of recognizing patterns. Keep in mind that more than one sequence may share the first few terms, so there is not one right answer for a problem like this. Any explicit formula for which the first given terms are correct is an acceptable formula. In fact, in some cases, the same sequence may be given by more than one explicit formula. Mathematical induction requires creativity.
It is often useful to be able to calculate the sum of the terms in a sequence.
The sum of the terms in a sequence is called a series. An infinite
series is the sum of the terms in an infinite sequence. A finite series
is the sum of the terms in a finite sequence. To express series conveniently,
we use summation notation. It looks like this: 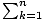 ak = a1 + a2 + a3 + ... + an. The index of summation is k. This equation might
be read "The sum of the terms of ak as k goes from 1 to n". an is a
sequence, and the summation of the sequence is a series.
ak = a1 + a2 + a3 + ... + an. The index of summation is k. This equation might
be read "The sum of the terms of ak as k goes from 1 to n". an is a
sequence, and the summation of the sequence is a series.
The following facts are true of summation notation, where ai and bi are sequences and c is a constant:
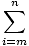 cai = c× cai = c×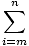 ai ai |
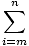 (ai±bi) = (ai±bi) = 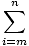 ai± ai±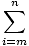 bi bi |
Some infinite series approach limits as n→∞, and others don't. Those that do approach a limit are called convergent series, and those that don't are called divergent series. Divergent series sometimes increase without bound, sometimes decrease without bound, and other times oscillate between values without approaching a single limit. Deciding whether an infinite series diverges or converges is a topic in calculus.
Certain sequences can be defined a third way, besides by an explicit formula or by listing the first few terms of the sequence. A recursive sequence is a sequence in which the nth term can be expressed as a function of the previous term. Such a sequence can be defined recursively by stating two things: the first term, and a formula in which an+1 is defined in terms of an. Two common forms of recursive sequences are arithmetic sequences and geometric sequences. They will be the topics of discussion in the next two sections.













