-
Amplitude
One-half the distance between the minimun and maximum value of a periodic function.
-
Coterminal
Having the same terminal side (a property of angles).
-
Identity
An equation containing one or more trigonometric functions which are true regardless of the angle used.
-
Initial Side
The side of an angle from which the rotation begins, or the initial position of the ray whose rotation creates the angle.
-
Inverse Trigonometric Function
The inverses of the six trigononometric functions with specific restricted ranges. They are arcsine, arccosine, arctangent, arccosecant, arcsecant, and arccotangent.
-
Period
The repeating interval of a periodic function; the period of a function is a real number.
-
Quadrant
One of the four regions in the coordinate plane created by the intersection of the axes.
-
Quadrantal Angle
An angle in standard position whose terminal side lies along one of the axes.
-
Radian
A unit of measure for angles. One revolution equals 2Π radians. A radian is also the measure of the central angle that intercepts an arc of the same length as the radius.
-
Reference Angle
The positive acute angle formed between the terminal side of an angle and the x-axis.
-
Standard Position
The location of an angle such that its vertex lies at the origin and its initial side lies along the positive x-axis.
-
Terminal Side
The side of an angle after rotation; the final position of the ray whose rotation created an angle.
-
Trigonometric Functions
Sine, cosine, tangent, cosecant, secant, and cotangent are the six trigonometric functions.
-
Vertex
The common endpoint of two rays that form an angle.
Terms
Formulae
| arccosecant | y = arccsc(x) = csc-1(x). Another way to write x = csc(y). |
| arccosine | y = arccos(x) = cos-1(x). Another way to write x = cos(y). |
| arccotangent | y = arccot(x) = cot-1(x). Another way to write x = cot(y). |
| arcsecant | y = arcsec(x) = sec-1(x). Another way to write x = sec(y). |
| arcsine | y = arcsin(x) = sin-1(x). Another way to write x = sin(y). |
| arctangent | y = arctan(x) = tan-1(x). Another way to write x = tan(y). |
| Cosecant |
Given a point P(x, y) on the terminal side of an angle θ in
standard position, distance d from the origin, its cosecant is
csc(θ) = 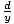 = = 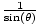 . .
|
| Cosine |
Given a point P(x, y) on the terminal side of an angle θ in
standard position distance d from the origin, its cosine is cos(θ) = 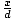 . .
|
| Cotangent |
Given a point P(x, y) on the terminal side of an angle θ in
standard position, its cotangent is cot(θ) = 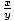 = = 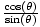 . .
|
| Secant |
Given a point P(x, y) on the terminal side of an angle θ in
standard position, distance d from the origin, its secant is sec(θ) = 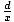 = = 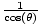 . .
|
| Sine |
Given a point P(x, y) on the terminal side of an angle θ in
standard position, distance d from the origin, its sine is sin(θ) = 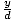 . .
|
| Tangent |
Given a point P(x, y) on the terminal side of an angle θ in
standard position, its tangent is tan(θ) = 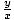 = = 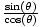 . .
|













