The Law of Cosines states the following:
Alternative versions look like this:
In the last two formulas, the parts are simply interchanged to make the law
easier under our convention of using
a,
b,
c,
A,
B, and
C to
label triangles. The Law of Cosines is only one formula, not three.
This law is used primarily in two situations: when two sides and their included
angle are given, and when three sides are given.
If two sides and their included angle are given, the next thing to calculate is
the third side. The Law of Cosines, as shown above, is perfect for the
situation. After the third side is calculated, the Law of Sines can be used
to calculate either of the other two angles.
If three sides are given, the Law of Cosines must be manipulated a bit: For
this situation, the Law of Cosines is most useful in this form:
cos(A) =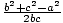 
. Once one of the angles is known, the next can be
calculated using the Law of Sines, and the third using subtraction, knowing that
the angles of a triangle sum to 180 degrees.
