Previous Next

Problem : Solve the following equation: sin(x)tan(x) = 0.

Solving sin(x) = 0, x = 0, Π. Solving tan(x) = 0, the same solutions are reached. x = 0, Π.

Problem : Solve the following equation: cos(x) - tan2(x) = 1.

Using the identity 1 + tan2(x) = sec2(x), the equation cos3(x) = 1 results. Therefore cos(x) = 1, and x = 0.

Problem : Solve the following equation: sin2(x) - 1 = cos2(x) + 2.

Using the identity sin2(x) + cos2(x) = 1, the equation sin2(x) = 2 results. This equation has no solution.

Problem : Solve the following equation: 2 sec(x)sin3(x) = 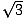cos(x)tan2(x).

Resolving everything into sines and cosines and then cancelling, we have sin(x) = . x = ,.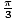

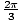
Problem : Solve the following equation: sin(x) + sin(x)cot2(x) = sec2(x) - tan2(x).

Factoring on the right side and the use of identities leads to the equations sin(x) = 1. Therefore, x = .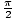
Previous section Next section

Take a Study Break