Using the eight fundamental identities and the six negative angle identities, an
infinite number of new identities can be created. Remember, a trigonometric identity
is any equation involving trigonometric functions
and which is true for any angle.
Study how to prove that the following equation is an identity by simplifying it using
the eight fundamental identities:
tan(θ)cos(θ) + 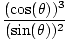 = sin(θ) + (csc(θ))2cos(θ) - cot(θ)sin(θ) = sin(θ) + (csc(θ))2cos(θ) - cot(θ)sin(θ) |
|
sin(θ) + 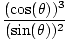 = sin(θ) + = sin(θ) + 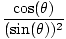 - cos(θ) - cos(θ) |
|
(cot(θ))2cos(θ) = cos(θ)(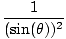 - 1) - 1) |
|
| (cot(θ))2cos(θ) = cos(θ)((csc(θ))2 - 1) |
|
| (cot(θ))2cos(θ) = cos(θ)(cot(θ))2 |
|
In general, it is helpful to follow these steps to simplify a potential identity:
- Express everything in terms of sine
and cosine.
- Cancel all terms possible.
- Rewrite the remaining expressions using as few trigonometric expressions as possible
(this will likely
involve converting sines and cosines to tangents,
secants, etc.)
- Factor anything that will result in one of the addition identities.
In following these steps, as we did in the example above, simplifying most equations will become easy.