Now we have both a definition of force, and a vague idea of how forces relate to motion. What we need is a precise way of relating the two. But even before we do this, we need to define another concept that plays a role in the relation between force and motion, that of mass.
Mass
Mass is defined as the amount of matter in a given body. This definition seems a little vague, and needs some explanation. Mass is a scalar quantity, meaning it has no direction, and is a property of the object itself, not its location. Mass is measured in kilograms (kg). Given a certain object, its mass will be the same on earth, on the moon, or in empty space. In contrast, the weight of the object in these different circumstances will change. We will explore further the relation between mass and weight when we have completed discussing Newton's laws. Yet even without a complete understanding of weight we can use weight to better understand the concept of mass. In our everyday experience, the heavier an object is (the more weight it has), the more mass it has. Thus our experience tells us that a baseball has more mass than a balloon, for example. As long as we do not think of them as the same concept, describing mass in terms of weight allows us to conceptualize mass in practical terms. From this concept of mass, we can more exactly relate force and motion.
Given a certain force, how does an object's motion correspond to its mass? Our intuition tells us that a more massive object moves slower if given the same force as a less massive object. We can throw a baseball with much greater speed than we can throw a massive ball of lead. Our intuition is correct, and is stated in Newton's Second Law.
Newton's Second Law
Newton's Second Law gives us a quantitative relation between force and motion:
secondlaw
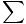 F = ma F = ma |
Stated verbally, Newton's Second Law says that the net force (F) acting upon an object causes acceleration (a), with the magnitude of the acceleration directly proportional to the net force and inversely proportional to the mass (m). Learn it and love it. Like it or not, this equation will be used at almost all times in virtually every physics course you take.
The Second Law relates two vector quantities, force and acceleration. Because both force and acceleration are vector quantities, it is important to understand that the acceleration of an object will always be in the same direction as the sum of forces applied to the object. The magnitude of acceleration depends on the mass of the object, but is always proportional to the force. Newton's Second Law gives an exact relation between the vectors force and motion. Thus we can use this law to predict the motion of an object given forces acting upon it, on a quantitative level.
Free Body Diagrams
The best method for calculating acceleration from force is through a free body diagram. This process, though fairly complicated, is extremely useful. We will go through it step by step:
- Step 1: Draw the physical situation in which an object exists. It may lie on an incline, be attached to a string, or simply be resting on the ground. Whatever the situation, draw it complete with any angles or distances that apply.
- Step 2: From the center of the body being examined, draw vectors representing each force acting upon the body, giving the magnitude of each one.
- Step 3: Sum all horizontal components of forces acting upon the object (this may require resolving a vector into its components (see Vectors).
- Step 4: Sum all vertical components of forces acting upon the object (using the same method as step 3).
- Step 5: Find the net force acting on the object, using the sum of the vectors found in steps 3 and 4.
- Step 6: Divide the net force by the object's mass to find the acceleration vector of the object.
- Step 7: From the acceleration vector, compute velocity, position, or any other necessary kinematic quantity.
There we have it! Finally, we can compute an exact relation between force and motion. With Newton's second law, we can take a given physical situation and find the acceleration, and thus the motion, of an object in the situation. In addition, using the method of free-body diagrams, we can evaluate any number of distinct forces. Such an ability is powerful, and will be used over and over in physics courses. We can now move on to Newton's Third Law, which further clarifies the nature of forces.













