Problem :
A 2 kg ball on a string is rotated about a circle of radius 10 m. The maximum tension allowed in the string is 50 N. What is the maximum speed of the ball?
The centripetal force in this case is provided entirely by the tension in the string. If the maximum value of the tension is 50 N, and the radius is set at 10 m we only need to plug these two values into the equation for centripetal force:
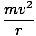 implies that v =
implies that v = 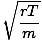
thus
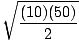 = 15.8 m/s
= 15.8 m/s
Problem :
During the course of a turn, an automobile doubles its speed. How much additional frictional force must the tires provide if the car safely makes around the curve?
Since Fc varies with v2, an increase in velocity by a factor of two must be accompanied by an increase in centripetal force by a factor of four.
Problem :
A satellite is said to be in geosynchronous orbit if it rotates around the earth once every day. For the earth, all satellites in geosynchronous orbit must rotate at a distance of 4.23×107 meters from the earth's center. What is the magnitude of the acceleration felt by a geosynchronous satellite?
The acceleration felt by any object in uniform circular motion is given by
a = 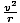 . We are given the radius but must find the velocity of the
satellite. We know that in one day, or 86400 seconds, the satellite travels
around the earth once.
Thus:
. We are given the radius but must find the velocity of the
satellite. We know that in one day, or 86400 seconds, the satellite travels
around the earth once.
Thus:
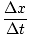 =
= 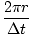 =
= 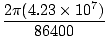 = 3076 m/s
= 3076 m/s
thus
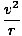 =
= 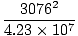 = .224 m/s2
= .224 m/s2
Problem :
The maximum lift provided by a 500 kg airplane is 10000 N. If the plane travels at 100 m/s, what is its shortest possible turning radius?
Again, we use the equation Fc =  . Rearranging, we find that
r =
. Rearranging, we find that
r = 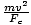 . Plugging in the maximum value for the lift of the plane,
we find that
. Plugging in the maximum value for the lift of the plane,
we find that
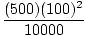 = 500m
= 500m
Problem :
A popular daredevil trick is to complete a vertical loop on a motorcycle. This trick is dangerous, however, because if the motorcycle does not travel with enough speed, the rider falls off the track before reaching the top of the loop. What is the minimum speed necessary for a rider to successfully go around a vertical loop of 10 meters?
During the entire trip, the rider experiences two different forces: the normal force from the track, and the gravitational force. At the top of the loop, both these forces point down, or towards the center of the loop. Thus the combination of these forces provides the centripetal force at that point. At the minimum speed of the motorcycle, however, he experiences no normal force. One can see this by envisioning that if the rider had gone any slower, he would have fallen off the track. Thus, at the minimum speed, all the centripetal force is provided by gravity. Plugging into our equation for centripetal force, we see that
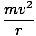
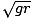 =
= 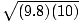 = 9.9 m/s
= 9.9 m/s













