What happens when a group of particles are all interacting? Qualitatively speaking, each exerts equal and opposite impulses on the other, and though the individual momentum of any given particle might change, the total momentum of the system remains constant. This phenomenon of momentum constancy describes the conservation of linear momentum in a nutshell; in this section we shall prove the existence of the conservation of energy by using what we already know about momentum and systems of particles.
Momentum in a System of Particles
Just as we first defined kinetic energy for a single particle, and then examined the energy of a system, so shall we now turn to the linear momentum of a system of particles. Suppose we have a system of N particles, with masses m1, m2,…, mn. Assuming no mass enters or leaves the system, we define the total momentum of the system as the vector sum of the individual momentum of the particles:
| P | = | p1 + p2 + ... + pn | |
| = | m1v1 + m2v2 + ... + mnvn |
Recall from our discussion of center of mass that:
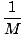 (m1v1 + m2v2 + ... + mnvn)
(m1v1 + m2v2 + ... + mnvn)
| P = Mvcm |
Thus the total momentum of the system is simply the total mass times the velocity of the center of mass. We can also take a time derivative of the total momentum of the system:
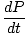 = M
= M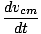 = Macm
= Macm
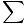 Fext = Macm
Fext = Macm
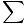 Fext = Fext = 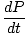 |
Don't worry if the calculus here is complex. Though our definition of the momentum of a system of particles is important, the derivation of this equation only matters because it tells us a great deal about momentum. When we explore this equation further we will generate our principle of conservation of linear momentum.
Conservation of Linear Momentum
From our last equation we will consider now the special case in which  Fext = 0. That is, no external forces act upon an isolated system of
particles. Such a situation implies that the rate of change of the total
momentum of a system does not change, meaning this quantity is constant, and
proving the principle of the conservation of linear momentum:
Fext = 0. That is, no external forces act upon an isolated system of
particles. Such a situation implies that the rate of change of the total
momentum of a system does not change, meaning this quantity is constant, and
proving the principle of the conservation of linear momentum:
When there is no net external force acting on a system of particles the total momentum of the system is conserved.
It's that simple. No matter the nature of the interactions that go on within a given system, its total momentum will remain the same. To see exactly how this concept works we shall consider an example.
Conservation of Linear Momentum in Action
Let's consider a cannon firing a cannonball. Initially, both the cannon and the ball are at rest. Because the cannon, the ball, and the explosive are all within the same system of particles, we can thus state that the total momentum of the system is zero. What happens when the cannon is fired? Clearly the cannonball shoots out with considerable velocity, and thus momentum. Because there are no net external forces acting on the system, this momentum must be compensated for by a momentum in the opposite direction as the velocity of the ball. Thus the cannon itself is given a velocity backwards, and total momentum is conserved. This conceptual example accounts for the "kick" associated with firearms. Any time a gun, a cannon, or an artillery piece releases a projectile, it must itself move in the direction opposite the projectile. The heavier the firearm, the slower it moves. This is a simple example of the conservation of linear momentum.
By both examining the center of mass of a system of particles, and developing the conservation of linear momentum we can account for a great deal of motion in a system of particles. We now know how to calculate both the motion of the system as a whole, based on external forces applied to the system, and the activity of the particles within the system, based on momentum conservation within the system. This topic, dealing with momentum, is as important as the last one, dealing with energy. Both concepts are universally applied: while Newton's Laws apply only to mechanics, conservation of momentum and energy are used in relativistic and quantum calculations as well.


 payment page
payment page



