Problem : A laserbeam strikes a vertical surface at an angle of 48o. The reflected beam can be seen as a spot on a horizontal surface. The spot is 10 meters away from the point of incidence on the vertical surface. How far is the horizontal distance from the spot to the vertical surface?
The angle of reflection is equal to the angle of incidence, so it is 48o. Thus the angle between the vertical surface and the reflected beam is 90 - 48 = 42o. The reflected beam is 10 meters long so its horizontal projection is given by 10 sin(42o) = 6.7 meters.Problem : In a dark room a beam enters through a pinhole 5 meters above the floor, reflects off a mirror 2 meters from the wall where it entered, and then forms a spot on the opposite wall 2.5 meters from the floor. How wide is the room?
The angle between the beam and the floor is given by tan-1(5/2) = 68.2o. Thus the angle of incidence is the complement of this, 21.8o. This is equal to the angle of reflection, so the angle between the floor and the reflected beam is also 68.2o. To find the distance from the point of incidence to the far wall we have tan(68.2o) = 2.5/dâá’d =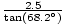 = 1. Therefore the room is 1 + 2 = 3 meters wide.
= 1. Therefore the room is 1 + 2 = 3 meters wide.
Problem : A mirror on a wall reflects sunlight onto the floor. The mirror is oriented vertically, directly facing the sun and has dimensions 0.7 meters × 0.7 meters, with its base 1 meter from the floor. If the sun if 50 meters above the horizon, how large is the patch of sunlight on the floor?
Light hitting the top of the mirror will have an angle of incidence of 50o, so the beam will make a 40o angle with the wall. This is 1.7 meters from the ground, so the beam will hit the floor 1.7 tan(40o) = 1.43 meters away from the wall. All the same angles are involved for light hitting the bottom of the mirror, except now the floor is only 1 meters away. Thus, this beam hits the floor tan(40o) = 0.84 meters from the wall. Thus one side of the patch is 1.43 - 0.84 = 0.59 meters long. The other dimension will be the same as that of the mirror, so the dimensions of the patch are 0.7×0.59 meters.Problem : Two mirrors are oriented at right angles to one another, forming a so-called corner reflector. Prove that the path of the light entering this system is antiparallel to the path of the light leaving the system.
Suppose the light is incident on the first mirror at some angle θi with respect to the normal to the surface. It reflects from the first mirror at this same angle. Since the mirrors are perpendicular, their normals must be perpendicular also, so the triangle formed by the intersecting normals and the light ray going between the mirrors is a right triangle with one angle θi. Since the sum of the angles of a triangle add to 90o the other angle must be 90o - θi. This is the angle of incidence on the second mirror, so it is also the angle of reflection from the second mirror. The angle between the incoming and outgoing waves is just the sum of the four incident and reflected angles, so we have θi + θi +90o - θi +90o - θi = 180o, hence the rays are antiparallel.Problem : What happens if we modify the situation in the previous problem (two plane mirrors oriented at right angles) to some angle μ < 90o between the mirrors. What is the angle between the incoming and outgoing rays in this case (limited to cases where only two reflections occur)?
Call the initial angle of incidence θi. The two mirrors along with their two normals form a quadrilateral containing two right angles and the angle μ, where the mirrors meet. Since the angles of a quadrilateral must add to 360o, the angle between the normals is 180o - μ. The two normals and the ray between the mirrors form a triangle, with one angle being that between the normals, another the angle of reflection from the first mirror, and the third the angle of incidence onto the second mirror. The first two of these are known, so if θ2 is the angle of incidence to the second mirror we can write: 180o - μ + θi + θ2 = 180o (angles of a triangle add to 180o). Thus θ2 = μ - θi. The angle of reflection from the second mirror is equal to the angle of incidence. Again adding up the four angles between the incoming and outgoing rays we have: 2×(θi) + 2×(μ - θi) = 2μ. This reduces correctly to the case we proved in the previous problem when μ = 90o.












