Geometric Optics

When the size of the physical and optical objects of a system are much larger than the wavelength of the light (or as λ→ 0), we are in the realm of geometrical optics. Optical systems in which the wave nature of light must be taken into account (interference, diffraction) are called physical optics. Of course, every real system experiences diffraction effects, so geometric optics is necessarily an approximation. However, the simplicity arising from treating only rays which move in straight lines affords many uses.

A lens is a refracting device (a discontinuity in the medium) that redistributes the energy being propagated by electromagnetic radiation. This is usually achieved by re-shaping the wavefront, most usefully by turning spherical waves into plane waves and vice-versa. Lenses that cause an incoming plane wave to bend towards the axis through its middle are called converging or convex lenses. They are thicker at their midpoint than at their edges. Concave lenses, on the other hand, are thicker at their edges than in the middle; they cause an incoming plane wave to bend away from its central axis and are hence also known as a diverging lenses. Both of these are illustrated in . For a converging lens, the point to which a plane wave converges is called the focal point or focus. For a diverging lens, it is the point from which incoming spherical waves must emerge in order to produce plane waves upon passing through the lens.

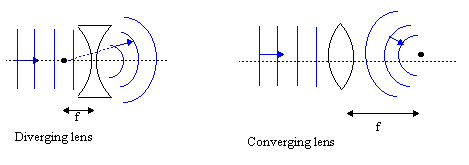
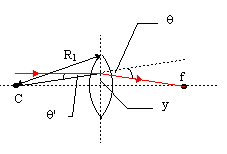
Lenses that have only two refracting surfaces are called simple. Also, lenses that have a thickness that is negligible compared to the overall path length of the light traversing them are called thin. Here we will only consider thin, simple lenses. To first-order, the focal length of such a lens is given by:

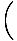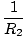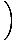where n_l is the index of refraction of the lens, R₂ is radius of curvature of the left surface (from which the light approaches), and R₁ is the radius of curvature of the right surface (through which the light leaves the lens). This is known as the lens-maker's equation. We can derive it by considering a spherical wave emanating from the center of the sphere with the same radius R₁ as one side of the lens. From it is clear that tanθ' = y/R₁. But since the angle θ' is small in the thin lens approximation, we can say θ' = y/R₁. Using a small angle approximation to Snell's Law we can write n_lθ' = θ, and thus the downwards deflection of the ray is θ - θ' = (n_l -1)θ' = (n_l -1)y/R₁. The distance at which this ray intersects the axial line must be the focal length and is given by: f = y/(θ - θ') = R₁/(n₁ - 1). If we consider a convex lens, a system of two plano-convex (planar on one side) lenses, we can use the formula that 1/f = 1/f₁ +1/f₂ to arrive at the lens-makers equation.

By far the most important formula in geometrical optics, however, relates the position of an object placed in front of a lens to the position of its image, formed by the lens. In the distance between the object and the lens is s_o and the distance between the lens and the image is s_i. Then

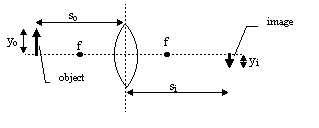
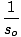There are certain sign conventions to be applied with this formula, and with those to follow. s_o > 0 if the object is on the same side of the lens as the direction from which the light is coming, s_o < 0, otherwise. f > 0 if the focal point is on the opposite side of the lens to that from which the light is coming. s_i < 0 if the image is on the opposite side of the lens to that from which the light is coming. R > 0 if the center of the sphere is on the opposite side of the lens to that from which the light is coming. The height of an object, y_o, or its image, y_i, is considered positive if it lies above the optical axis (the central axis or axis of symmetry of the lens). Note that a planar interface has a focal length of infinity. The "transverse magnification" of a thin lens is given by:

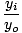From the sign conventions, M_T > 0 implies that the image is upright, while M_T < 0 implies that it is inverted.

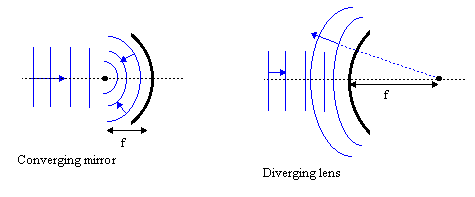
There are also two basic types of spherical mirrors. Concave mirrors reflect incoming plane waves to a focal point directly in front of the mirror (they are converging mirrors). Convex mirrors reflect incoming plane waves into outward-moving spherical waves with the center of the sphere appearing to be behind the mirror (they are diverging mirrors). The focal length of a mirror is f = - , where R is the radius of curvature of the mirror. Also the very same relation between the image and object distances applies:

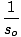Applying the sign conventions that f, s_o, and s_i are positive in front of the mirror, f > 0 for concave mirrors and f < 0 for convex mirrors. Note that images for which s_i is positive are called real images, and are those for which a screen can be placed at the position of the image in order to observe it; images for which s_i is negative are called virtual. No virtual image can be formed on a screen--any image seen in a mirror is an example of a virtual image. An alternative formulation of these definitions is to say that for real images light rays really do pass through where the image forms; for virtual images light rays only appear to be coming from the position of the image.

Mirrors have an advantage over lenses in that they do not suffer chromatic aberration. This phenomenon arises due to dispersion, causing the lens to have not just one focal length but a small band of focal lengths corresponding to the different amounts by which it refracts the different colors. This means that it is impossible to focus colored images precisely with a lens. Mirrors, because they do not rely on refraction, do not suffer this problem. Moreover, it is important to remember that all the formulas we encountered here were derived using the first order approximation to the sine function appearing in Snell's Law: sinθ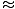 θ. Of course this ignores higher order terms in θ³, etc. Corrections arising from this and other considerations cause aberrations (or deviations) from the simple equations developed here for spherical lens and mirror systems. In fact, there are five primary, monochromatic aberrations called spherical aberration, coma, astigmatism, field curvature, and distortion. They are collectively known as the Seidel aberrations.

Often it will be useful to determine the approximate position of an image, given the position of the object and the focal length in a lens or mirror system without resorting to the lens equation. We can do this by drawing diagrams and mapping out the path of the light rays. This process is known as analytical ray tracing. The basic strategy is to select a significant point on the object (like the top) and to draw several principal rays from that point. For a mirror, the three principle rays, shown in , are: i) parallel to the axis, returning through the focal point; ii) to the midpoint of the mirror, reflecting at an equal angle on the opposite side to the central axis; and iii) through the center of the sphere of which the mirror is a part, returning along the same path. The principal rays for a lens are similar: i) parallel to the central axis, refracting through the focal point; ii) a straight ray through the center of the lens; and iii) through the focal point on the near side, refracting parallel to the axis. At least two principal rays must be drawn from the object; the point where the principal rays cross (or appear to cross, for a virtual image) is the location of the image. To determine whether an object is magnified or diminished, it would be necessary to choose one other point (such as the base) and compare this distance between the two points in the image to their positions in the object. To find the locations of virtual images it is necessary to trace the light rays backwards behind the mirror or lens.

Ray tracing is especially useful when complicated systems of mirrors and/or lenses need to be analyzed. Ray tracing can give a rough but quick idea of how the system will behave. For example, it can fairly quickly be determined that a single concave lens will always produce virtual, diminished, upright images, irrespective of the position of the object. However, for a convex lens, the location of the image depends on the location of the object. Recall that real objects and real images have s_o > 0, or s_I > 0, while these distances are negative for virtual objects and images (virtual objects can arise when the image for one lens becomes the object for another in a lens system). f > 0 corresponds to converging lenses or mirrors and f < 0 corresponds to diverging lenses or mirrors. Positive y_o or y_i correspond to upright objects and images respectively. A negative magnification corresponds to an inverted image.