Linear Polarization and Natural Light
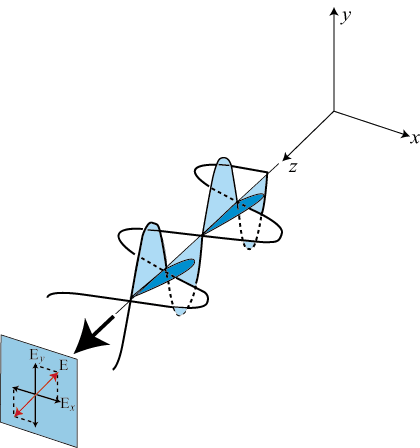
Light, as we have said, is a transverse electromagnetic wave. However, until this point we
have only considered light for which the electric (and magnetic) field vector are oscillating in a single, fixed
plane. Such light is called linearly polarized or plane polarized. In other words, although the
electric field oscillates in magnitude and sign, its orientation is constant. A fixed plane of vibration
contains both E and 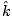 , the direction of propagation. However, natural light is
generated by a large number of randomly oriented atomic oscillators. The light emitted from these
oscillators will combine momentarily to form a linearly polarized wave, but this will persist for no
longer than 10-8 seconds before different atomic oscillators emit new randomly polarized waves
causing a different polarization of the resultant wave. The result is that the polarization of natural light
fluctuates too rapidly to be detectable. This situation is called random polarization. In most light
the polarization is neither completely random nor completely linear -- this is known as partially polarized
light.
, the direction of propagation. However, natural light is
generated by a large number of randomly oriented atomic oscillators. The light emitted from these
oscillators will combine momentarily to form a linearly polarized wave, but this will persist for no
longer than 10-8 seconds before different atomic oscillators emit new randomly polarized waves
causing a different polarization of the resultant wave. The result is that the polarization of natural light
fluctuates too rapidly to be detectable. This situation is called random polarization. In most light
the polarization is neither completely random nor completely linear -- this is known as partially polarized
light.
Consider two plane polarized waves propagating in the z direction, one oscillating in the x-direction and one in the y-direction:
| Ex(z, t) | = 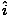 E0xcos(kz - σt) E0xcos(kz - σt) | ||
| Ey(z, t) | = 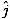 E0ycos(kz - σt + ε) E0ycos(kz - σt + ε) |
In this case Ey lags Ex by ε > 0. For ε = 0,±2Π,±4Π, etc. the resultant wave is (by superposition):
E[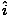 E0x + E0x + 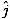 E0y]cos(kz - σt) E0y]cos(kz - σt) |
As shown in this wave has a constant amplitude but is tilted at an angle θ = tan-1
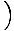 with respect to the x-axis. The wave is still linearly
polarized. If E0x = E0y it is polarized at 45o to the original waves. If ε is an
odd integer multiple of Π then the wave is still linearly polarized but now has amplitude
with respect to the x-axis. The wave is still linearly
polarized. If E0x = E0y it is polarized at 45o to the original waves. If ε is an
odd integer multiple of Π then the wave is still linearly polarized but now has amplitude
 E0x -
E0x -  E0y which corresponds to a rotation of 2θ.
E0y which corresponds to a rotation of 2θ.
It is also possible for light to what is called circularly polarized. This occurs when E0x = E0y = E0 (in the case where the amplitudes are not equal the polarization is elliptical) and the phase difference between the component waves is ε = - Π/2±2Πm for m any integer. The resulting equation for the wave is:
E = E0[ cos(kz - σt) + cos(kz - σt) + 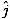 cos(kz - σt)] cos(kz - σt)] |
The amplitude of the wave is now a constant but the direction of E varies in time. In fact, the electric field vector is rotating clockwise at an angular frequency σ (as seen by an observer toward whom the wave is moving). This is called right-circularly polarized light. Left-circularly polarized light has an electric field vector that rotates counterclockwise, and corresponds to phase differences of ε = Π/2±2Πm.
Polarizing substances
A device which creates polarized light when natural light is incident upon it is called a polarizer. Polarizers work by one of four methods: selective absorption, reflection, scattering, or birefringence. For a linear polarizer, only light with a polarization parallel to a particular axis will be transmitted; this axis is called the transmission axis. Rotating the polarizer when natural light is incident will have no effect on the irradiance on the far side of the polarizer because of the random polarization of the light. However, if a second identical polarizer is placed behind the first and rotated with respect to the first, the irradiance will vary. This is because light passing through the first polarizer will be plane polarized. As the transmission axis of the second polarizer or analyzer is rotated only the component of the plane polarized light parallel to this axis will be transmitted. When the angle between the two polarizers reaches 90o the plane polarized light has no component parallel to the transmission axis of the analyzer. For angles in between the irradiance of the transmitted light is given by Malus' Law:
| I = I0cos2θ |
where I0 is the maximum irradiance.
The simplest polarizer is called a wire-grid polarizer and consists simply of a number of closely spaced
parallel wires.
The related phenomenon of birefringence occurs when a substance is optically anisotropic, or does not have the same optical properties in all directions. Most usually, this manifests itself as the property that light travels faster through the substance along one axis than it does along another. Thus the substance has two different refractive indices (refringence is an old word for refraction). This can arise from a difference in how strongly electrons in the atoms in the crystal structure are bound to their nucleus; electrons along one axis may be bound more strongly causing them to have a different resonance frequency (see the discussion of dependence on index of refraction on frequency).
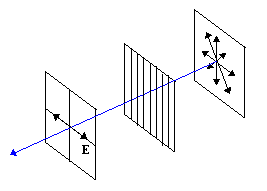
Polarization by Scattering and Reflection
Scattering occurs when an incident light wave causes a dipole to vibrate in the direction
parallel to the electric field. The dipole does not radiate in the direction in which it is oscillating.
Reflection from dielectric surfaces also causes polarization. For electric fields polarized
perpendicular to the plane of incidence (the plane of the incoming ray) the reflected and
transmitted waves must also be polarized in the same direction as the incident wave. However, for E
in the plane of incidence the electron-oscillators on the surface of the dielectric will vibrate
under the influence of the refracted wave. However, shows the
angle between the reflected wave and the dipole axis (the direction of oscillation) is now small
and thus very little light will be reflected in this direction.
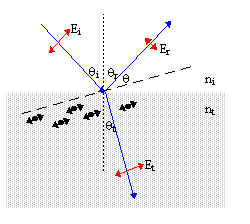
tanθp = 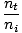 |
For unpolarized light incident on the surface at Brewster's angle, the reflected light is polarized perpendicular to the incident plane, or parallel to the surface. At other angles, the reflected light will be partially polarized.













