Problem :
Write down the Planck Distribution Function.
<
s > =
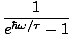
Problem :
Looking at the Planck distribution function, describe what happens at
the high and low frequency limits.
For τ
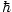 σ, the occupation of these low frequency states
is very high, approaching ∞. This poses no problem however
because it is the density of photons per frequency space that is
physically important, and so there are very few frequencies that have
this high occupancy.
σ, the occupation of these low frequency states
is very high, approaching ∞. This poses no problem however
because it is the density of photons per frequency space that is
physically important, and so there are very few frequencies that have
this high occupancy.
For τ
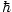 σ, the occupation of the high frequency states is
near zero.
σ, the occupation of the high frequency states is
near zero.
Problem :
Explain why there is a factor of 1/8 when we rewrite the sum as an
integral in our derivation of the Stefan-Boltzmann law of radiation.
When we are summing over quantum states, only non-negative quantum
numbers are allowed. Writing the integral alone sums over all 8
quadrants in n-space, and so we divide by 8 to get the right answer.
Problem :
Write down the Stefan-Boltzmann law of radiation.
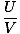
=
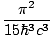 τ4
τ4
Problem :
Describe why it is reasonable to expect that the entropy of a photon gas
would go as τ3.
We saw that the energy goes as τ4, and we can recall that the
temperature can be defined as  with
appropriate variables held constant. The only way to satisfy such a
requirement is to have σ go as τ3.
with
appropriate variables held constant. The only way to satisfy such a
requirement is to have σ go as τ3.