The Boltzmann Factor
Suppose that we have two states accessible to a system. Let the energy
of the first be given by 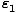 and the energy of the second be
given by
and the energy of the second be
given by  . It can be derived that the ratio of the
probabilities of occupation of the two states is given by:
. It can be derived that the ratio of the
probabilities of occupation of the two states is given by:
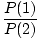
=
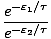
Any term of the form e- /τ is called a Boltzmann
Factor.
/τ is called a Boltzmann
Factor.
You may wonder why we cannot simply write P(1) = e-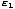 /τ.
The reason is that we are not guaranteed that the sum
of the probabilities is equal to one yet, and therefore we can only talk
of relative probabilities right now (see
Quantum). In order to speak of the
absolute probability we need to introduce a new concept.
/τ.
The reason is that we are not guaranteed that the sum
of the probabilities is equal to one yet, and therefore we can only talk
of relative probabilities right now (see
Quantum). In order to speak of the
absolute probability we need to introduce a new concept.
The Partition Fucntion
We define the partition function as follows:
Z =
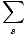 e-
e-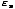 /τ
/τ
Notice that the partition function adds up all of the Boltzmann factors
for a system. We can use it to make a crucial statement about absolute
probability:
P(
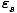
) =
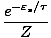
The equation should make sense to you. If the Boltzmann factor for a
particular state were 2, and the partition function were 5, then we
should expect our probability to by 0.4. Notice that P ranges from 0
to 1 as desired.