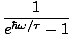Planck Distribution
We want to learn about the spectrum of thermal radiation in a cavity.
This doesn't sound familiar at first. We often call thermal radiation
"blackbody radiation", but we won't go into the terminology too much
here.
We know from our understanding of quantum mechanics
that photons are
quantized particles. Take any given mode, or frequency, of oscillation
in a cavity. Then we say that each mode can be occupied only by an
integral number of photons. In terms of energy, the allowable energies
for the mode of frequency σ are 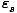 = s
= s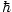 σ.
Here, we can think of s as being the number of photons in that mode.
σ.
Here, we can think of s as being the number of photons in that mode.
For a given frequency, then, we can calculate the partition
function:
Z =
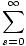 e-s
e-s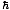 σ/τ
σ/τ
This, however, is just an expansion of a closed form:
Z =
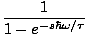
Now, we can find the average number of photons in a particular mode, or
< s >, using the formula for average value of a property:
Substituting in for Z and doing some unillustrative algebra yields the
final result:
<
s > =