Previous Next

The result is known as the Planck distribution function and gives us the average number of photons in the mode with frequency σ.

Stefan-Boltzmann Law

From the Planck distribution function, we can derive the energy density in the cavity. Convince yourself that the total energy in the cavity is given by:

U = < >

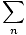
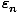
Each 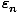corresponds to the energy at a particular frequency σn, and summing over all of the averages should yield the total energy. More explicitly:

U = < > = < s > σ =

Here, we can use the standard quantum method of letting the cavity be a cube and quantizing the frequencies to obtain σn = nΠc/L if L is the length of a side of the cube.

We need one more trick to complete the derivation. The sum over positive n in 3 dimensions becomes 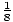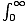4Πn2 dn. With those tools, we can plug through some more algebra to obtain:

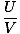
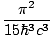= τ4

The result is known as the Stefan-Boltzmann law of radiation. The significant aspect of the formula is that the energy density is proportional to the fourth power of the temperature.

Previous page Thermal Radiation page 1 Next page Thermal Radiation page 3

Take a Study Break