Thermodynamics: Stats
Gibbs Sum
Gibbs Factor
We derived in Section 1 the Boltzmann factor by allowing the temperature to change. If we generalize and allow the number of particles to change as well, we can obtain a ratio of probabilities:
= 
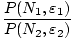
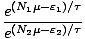
The structure of the above is very similar to what we encountered
before. Ignoring the new term returns the familiar form from before.
Any term of the form
e
(Nμ-
)/τ
is called a Gibbs
factor.
Gibbs Sum
So far we only have a mechanism for relative probabilities. To obtain absolute probabilities, we need to have a sum that adds up all of the Gibbs factors. This sum is called the Gibbs sum and is given by:
e
(Nμ-
)/τ
Note that in taking the sum we begin with
N = 0
, which has its own
corresponding energies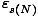
, and sum over all the states
with
N = 0
. Then we move to
N = 1
, and so on.
We can calculate the absolute probability of occupation of a state now using the Gibbs factor and the Gibbs sum just as we did with the Boltzmann factor and sum earlier.
