Previous Next

Alternate Definitions of Variables

We originally defined our variables in terms of U, but now that we have more expressions for the energy, we can devise new expressions of the variables as well.

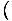
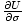
For example, we originally defined the temperature as τ = 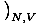. But we can also use the enthalpy identity to write τ = .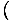

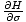
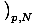It isn't hard to formulate these definitions on your own. Find an energy identity in which the variable you wish to define is free, and then take the other two differentials constant and solve. Say we wish to look at the entropy in terms of the Helmholtz free energy. We see that V and N are in differentials in F, and so we write: σ = - .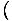

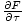
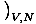Many other relations exist, but we will leave you to derive them on your own and in the problems at the end of the section. Again, understanding this fluidity and flexibility in definition will be key to solving problems efficiently.

Alternate Definitions Using the Energy

Above we showed how to define the variables in terms of the energy, but we can bypass the energy by keeping it constant. For example, suppose the energy U were held constant, as were the number of particles. Though we will gloss over some mathematics here, it seems plausible that you could then write: p = τ.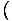

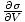
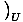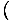
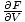
Moreover, we can use the definitions of the other energies to obtain more complex formulations of the variables. Take F = U - τσ. We know that p = - . We can take the derivative to obtain:

Previous section Next page Variables Revisited page 2

Take a Study Break