We saw in the previous section on dot products that the dot product takes two vectors and produces a scalar, making it an example of a scalar product. In this section, we will introduce a vector product, a multiplication rule that takes two vectors and produces a new vector. We will find that this new operation, the cross product, is only valid for our 3-dimensional vectors, and cannot be defined in the 2- dimensional case. The reasons for this will become clear when we discuss the kinds of properties we wish the cross product to have.
Rotational Invariance
One important feature of the dot product which we didn't mention in the previous section is its invariance under rotations. In other words, if we take a pair of vectors in the plane and rotate them both by the same angle (imagine, for instance, that the vectors are sitting on a record, and rotate the record), their dot product will remain the same. Consider the length of a single vector (which is given by the dot product): if the vector gets rotated about the origin by some angle, its length will not change--even though its direction can change quite dramatically! Similarly, from the geometric formula for the dot product, we see that the result depends only on the lengths of the two vectors and the angle between them. None of these quantities changes when we rotate the two vectors together, so neither can their dot product. This is what we mean when we say that the dot product is invariant under rotations.
Rotational invariance ends up being a very important property in physics. Imagine writing down vector equations to describe some physical situation taking place on a table. Now rotate the table (or keep the table fixed, and rotate yourself by some angle around the table). You haven't really changed anything about the physics on the table by simply turning everything by some fixed angle. Because of this, you should expect your equations to retain their form. This means that if these equations involve products of vectors, these products better be rotationally invariant. The dot product has already passed this test, as we noted above. We now want to require the same of the cross product.
Making the requirement of rotational invariance more stringent for the cross product, we need the cross product of two vectors to yield another vector. Consider, for instance, two 3-dimensional vectors u and v in a plane (two non-parallel vectors always define a plane, in the same way that two lines do. If we rotate this plane, the vectors will change direction, but we don't want the cross product w = u×v to change at all. However, if w has any non-zero components in the plane of u and v, those components will necessarily change under rotation (they get rotated just like everything else). The only vectors that won't change at all under a rotation of the u-v plane are those vectors that are perpendicular to the plane. Hence, the cross product of two vectors u and v must give a new vector which is perpendicular to both u and v.
This simple observation actually goes a long way towards constraining our options for how we can define the cross product. For instance, we can see immediately that it is not possible to define a cross product for two- dimensional vectors, since there is no direction perpendicular to the plane of two-dimensional the vectors! (We'd need a third dimension for that).
Now that we know the direction in which the cross product of two vectors points, the magnitude of the resulting vector remains to be specified. If I take the cross product of two vectors in the x-y plane, I now know that the resulting vector should point purely in the z-direction. But should it point upwards (i.e. lie along the positive z-axis) or should it point downwards? How long should it be?
Let's begin by defining the cross product for the unit vectors i, j, and k. Since all vectors can be decomposed in terms of unit vectors (see Unit vectors), once we've defined the cross products for this special case it will be easy to extend the definition to include all vectors. As we noted above, the cross product between i and j (since they both lie in the x-y plane) must point purely in the z-direction. Hence:
| i×j = ck |
for some constant c. Because later on we will want the magnitude of the resultant vector to have geometric significance, we need ck to have unit length. In other words, c can be either +1 or -1. Now we make a completely arbitrary choice in order to accord with convention: we choose c = + 1. The fact that we have chosen c to be positive is known as The Right-Hand Rule (we could just as easily have chosen c = - 1, and the math would all work out to be the same as long as we were consistent--but we do have to choose one or the other, and there's no use going against what everyone else does.) It turns out that in order to be consistent with the Right-Hand Rule, all of the cross products between unit vectors are uniquely determined:
| i×j | = | k = - j×i | |
| j×k | = | i = - k×j | |
| k×i | = | j = - i×k |
In particular, notice that the order of the vectors within the cross products holds significance. In general, u×v = - v×u. From here we can see that the cross product of a vector with itself is always zero, since by the above rule u×u = - u×u, which means that both sides must vanish for equality to hold. We can now complete our list of cross products between unit vectors by observing that:
| i×i = j×j = k×k = 0 |
To take the cross product of two general vectors, we first decompose the vectors using the unit vectors i, j, and k, and then proceed to distribute the cross product across the sums, using the above rules to do the cross products between unit vectors. We can do this for arbitrary vectors u = (u1, u2, u3) and v = (v1, v2, v3) to get a general formula:
| u | = | u1i + u2j + u3k | |
| v | = | v1i + v2j + v3k | |
| u×v | = | (u1i + u2j + u3k)×(v1i + v2j + v3k) | |
| = | u1v1(i×i) + u1v2(i×j) + u1v3(i×k) + ...(9 terms in all!) | ||
| = | (u1v2 - u2v1)k + (u3v1 - u1v3)j + (u2v3 - u3v2)i |
Unfortunately, this is as easy as it gets when it comes to writing out the cross product explicitly in terms of vector components. It is probably a good to keep this formula handy until you become used to computing vector cross products.
Geometric Formula for Cross Product
Fortunately, as is the case with the dot product, there is a simple geometric formula for computing the cross product of two vectors, if their respective lengths and the angle between them is known. Consider the cross product of two (not necessarily unit-length) vectors that lie purely along the x and y axes (as i and j do). We can thus write the vectors as u = ai and v = bj, for some constants a and b. The cross product u×v is thus equal to
| u×v = ab(i×j) = abk |
Notice that the magnitude of the resultant vector is the same as the area of the rectangle with sides u and v! As promised above, the magnitude of the cross product between two vectors, | u×v|, has a geometric interpretation. In general it is equal to the area of the parallelogram having the two given vectors as its sides (see ).
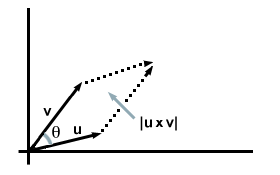
From basic geometry, we know that this area is given by area= | u|| v| sinθ, where | u| and | v| are the lengths of the sides of the parallelogram, and θ is the angle between the two vectors. Notice that when the two vectors are perpendicular to each other, θ =90 degrees, so sinθ =1 and we recover the familiar formula for the area of a square. On the other hand, when the two vectors are parallel, θ =0 degrees, and sinθ=0, meaning the area vanishes (as we expect). In general, then, we find that the magnitude of the cross product between two vectors u and v that are separated by an angle θ (going clockwise from u to v, as specified by the Right-Hand Rule) is given by:
| | u×v| = | u|| v| sinθ |
In particular, this means that for two parallel vectors the cross product equals 0.
Cross Product Summary
In summary, the cross product of two vectors is given by:
| u×v = (u1v2 - u2v1)k + (u3v1 - u1v3)j + (u2v3 - u3v2)i |
where the resultant vector is perpendicular to each of the original two and its magnitude is given by | u×v| = | u|| v| sinθ.













