payment page
Problem :
What is the kinetic energy of a 2 kg ball that travels a distance of 50 meters in 5 seconds?
The velocity of the ball is easily calculable: v =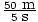 
= 10 m/s. With
values for the mass and velocity of the ball, we can calculate kinetic energy:
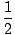mv2 = 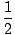(2 kg)(10 m/s)2 = 100 J
Problem :
In a sense we all have kinetic energy, even when we are standing still. The earth, with a radius of 6.37×106 meters, rotates about its axis once a day. Ignoring the earth's rotation about the sun, what is the kinetic energy of a 50 kg man standing on the surface of the earth?
To find the velocity of the man we must find how far he travels over a given
time period. In one day, or 86400 seconds, the man travels the circumference of
the earth, or 2Πr meters. Thus the velocity of the man is v =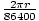 
= 
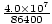= 463 m/s. Again, since we know the
velocity and mass of the man we can calculate kinetic energy.
K =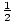 
mv2 = 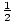(50 kg)(463 m/s)2 = 5.36×106
Joules.
Problem :
A ball is dropped from a height of 10 m. What is its velocity when it hits the ground?
The ball is acted upon by a constant gravitational force, mg. The work done during its total trip, then, is simply mgh. By the Work-Energy theorem, this causes a change in kinetic energy. Since the ball initially has no velocity, we can find the final velocity by the equation: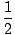mv2
Solving for v ,
= 
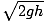= 14 m/s
Problem :
A ball is thrown vertically with a velocity of 25 m/s. How high does it go? What is its velocity when it reaches a height of 25 m?
The ball reaches its maximum height when its velocity is reduced to zero. This change in velocity is caused by the work done by gravitational force. We know the change in velocity, and hence the change in kinetic energy of the ball, and can calculate its maximum height from this:
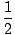mvf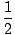2 - mvo2
But vf = 0 , and the masses cancel, so
= 
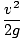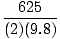= 31.9 m
When the ball is at a height of 25 meters, the gravitational force has done an amount of work on the ball equal to W = - mgh = - 25 mg. This work causes a change in velocity of the particle. We now use the Work-Energy Theorem, and solve for the final velocity:
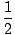mvf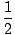2 - mvo2
Again, the masses cancel:
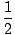vf2 = 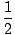vo2 - gh
Thus
= 
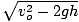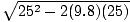= 11.6 m/s
Problem :
A ball with enough speed can complete a vertical loop. With what speed must the ball enter the loop to complete a 2 m loop? (Keep in mind that the velocity of the ball is not constant throughout the loop).
At the top of the loop, the ball must have enough velocity such that the centripetal force provided by its weight keeps the ball in circular motion. In other words:
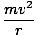
Solving for v ,
= 
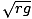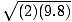= 4.4 m/s
During the entire vertical loop, the ball is acted upon by two forces: the normal force and the gravitational force. The normal force, by definition, always points perpendicular to the circumference of the loop, and thus the motion of the ball. Consequently, it cannot perform work on the ball. The gravitational force, on the other hand, does perform work on the ball, according the height it reaches. Since the radius of the circle is 2 m, the ball reaches a height of 4 m, and experiences work from the gravitational force of - mgh = - 2mg. Remember the sign is negative because the force acts in a direction opposite the motion of the ball. This work causes a change in velocity from the bottom of the loop to the top of the loop, which can be calculated by the work-energy theorem:
Thus
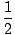mvf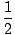2 - mvo2
Canceling the mass and solving for vo ,
= 
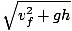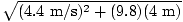= 7.7 m/s
