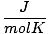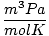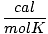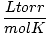Charles' Law
Charles' law states that, at a constant pressure, the volume of a mixed amount of gas is directly proportional to its absolute temperature:
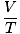 = k = k |
Where k is a constant unique to the amount of gas and pressure. Just as with Boyle's law, Charles' law can be expressed in its more useful form:
 = = 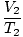 |
The subscripts 1 and 2 refer to two different sets of conditions, just as with Boyle's law.
Why must the temperature be absolute? If temperature is
measured on a Celsius (non absolute) scale, T can be negative. If we
plug negative values of T into the equation, we get back
negative volumes, which cannot exist. In order to ensure that only
values of V≥ 0 occur, we have to use an absolute temperature
scale where T≥ 0. The standard absolute scale is the Kelvin
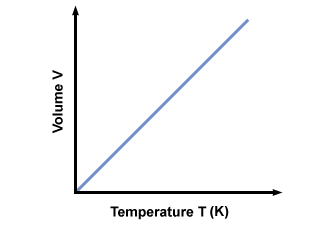
(K) scale. The temperature in Kelvin can be calculated via Tk = TC + 273.15. A plot of the temperature in Kelvin vs. volume
gives :
Avogadro's Law
Avogadro's law states that the volume of a gas at constant temperature and pressure is directly proportional to the number of moles of gas present. It's mathematical representation follows:
| fracVn = k |
k is a constant unique to the conditions of P and T. n is the number of moles of gas present.
1 mole (mol) of gas is defined as the amount of gas containing Avogadro's number of molecules. Avogadro's number (NA) is
| NA = 6.022×1023 |
1 mol of any gas at 273 K (0_C) and 1 atm has a volume of 22.4 L. The conditions 273 K and 1 atm are the standard temperature and pressure (STP). STP should not be confused with the less common standard atmospheric temperature and pressure (SATP), which corresponds to a temperature of 298 K and a pressure of 1 bar.
The numbers 22.4 L, 6.022×1023, and the conditions of STP should be near and dear to your heart. Memorize them if you haven't already.
The Ideal Gas Law
Charles', Avogadro's, and Boyle's laws are all special cases of the ideal gas law:
| PV = nRT |
T must always be in Kelvin. n is almost always in moles. R is the gas constant. The value of R depends on the units of P, V and n. Be sure to ask your instructor which values you should memorize.
| Units | Value of R | ||
| 0.08206 | ||
| 8.314 | ||
| 8.314 | ||
| 1.987 | ||
| 62.36 |
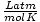 and 8.314
and 8.314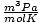 get the most use. Memorizing them will make your
life easier.
get the most use. Memorizing them will make your
life easier.
The ideal gas law is the equation you must memorize for gases. It not only allows you to relate P, V, n and T, but can replace any of the three classical gas laws in a pinch. For example, let's say you're given constant values of P and n, but forget how Charles' law relates V and T. Rearrange the ideal gas law to separate the constants and unknowns:
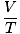 = =  = k = k |
Voila! We have derived Charles' law from the ideal gas law. n, R, and T are constants, so
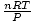 is just the
constant k from Charles' law.
is just the
constant k from Charles' law.
The ideal gas law is also useful for those rare occasion when you
forget the value of a constant. Let's say I forgot the value of R in
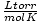 . If I remember that a mole of gas has a volume
of 22.4 L at STP (760 torr, 273 K), I can rearrange PV = nRT to
solve for R in the desired units. It is much more efficient to
memorize the values, but it is comforting to know that you can always
fall back on good old PV = nRT.
. If I remember that a mole of gas has a volume
of 22.4 L at STP (760 torr, 273 K), I can rearrange PV = nRT to
solve for R in the desired units. It is much more efficient to
memorize the values, but it is comforting to know that you can always
fall back on good old PV = nRT.
Applying the Ideal Gas Law
Ideal gas law problems tend to introduce a lot of different variables and numbers. The sheer amount of information can be confusing, and it is wise to develop a systematic method to solve them:
1) Jot down the values of P, V, n, and T. If the question says that one of these variables is constant or asks you to find the value of one or the other, make a note of it. Every time you encounter a numerical value or variable, try to fit it into your PV = nRT scheme.
2) Rearrange PV = nRT such that the unknowns and knowns are on opposite sides of the "=" sign. Make sure that you are comfortable with the algebra involved.
3) Convert to the appropriate units. Generally you'll want to deal with SI units (m3, Pa, K, mol). There will be times that non-SI units will be more convenient. In these cases, remember that T must always be in Kelvin. Make sure to select the correct value and units of R.
4) Plug in values and solve for the unknown(s). Ideal gas problems involve a great deal of algebra. The only way to master this type of problem is to practice. Use the problems provided at the end of this section and your textbook until the manipulations of PV = nRT become familiar.
5) Take a step back and check your work. The easiest way to do this is to carry all of the units through your ideal gas calculations. When you're about to solve the equation, make sure that the units on both sides of the "=" sign are equivalent. For simpler problems, it is also worthwhile to make sure that your answer makes sense. For example, if n, R, and T are constant and P rises, make sure that V decreases. It only takes a few seconds, and can save you from some embarrassing mistakes. The usefulness of such commonsense checks decreases as the questions get more complex. For any problem where more than two variables change, you're better off trusting the ideal gas law and your own algebra.
The best advice I can give you is to practice. The more problems you do, the more comfortable you will be with the ideal gas law.