Please wait while we process your payment
If you don't see it, please check your spam folder. Sometimes it can end up there.
If you don't see it, please check your spam folder. Sometimes it can end up there.
Please wait while we process your payment
Get instant, ad-free access to our grade-boosting study tools with a 7-day free trial!
Learn more



This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!

Annual
2-49 accounts
$22.49/year + tax
50-99 accounts
$20.99/year + tax
Select Quantity
Price per seat
$29.99 $--.--
Subtotal
$-.--
Want 100 or more? Request a customized plan
You could save over 50%
by choosing an Annual Plan!

SAVE OVER 50%
compared to the monthly price!
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
$22.49/month + tax
Save 25%
on 2-49 accounts
$20.99/month + tax
Save 30%
on 50-99 accounts
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!
You will only be charged after the completion of the 7-day free trial.
If you cancel your account before the free trial is over, you will not be charged.
You will only be charged after the completion of the 7-day free trial. If you cancel your account before the free trial is over, you will not be charged.
Order Summary
Annual
7-day Free Trial
SparkNotes PLUS
$29.99 / year
Annual
Quantity
51
PLUS Group Discount
$29.99 $29.99 / seat
Tax
$0.00
SPARK25
-$1.25
25% Off
Total billed on Nov 7, 2024 after 7-day free trail
$29.99
Total billed
$0.00
Due Today
$0.00
Promo code
This is not a valid promo code
Card Details
By placing your order you agree to our terms of service and privacy policy.
By saving your payment information you allow SparkNotes to charge you for future payments in accordance with their terms.
Powered by stripe
Legal
Google pay.......



Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Your PLUS subscription has expired
Please wait while we process your payment
Please wait while we process your payment

Problems
Problem : Blaise decides to build a barometer. He can't find any mercury in his workshop and decides to use water instead. Assume that the density of water is 1.00×103 kg/m3. If the atmospheric pressure is 7.60×102 torr, how tall must his barometer be in order to obtain an accurate reading?
First, convert the atmospheric pressure to Pascals. 7.60×102 torr = 101, 325 Pa. Now that all the variables are in SI units, rearrange P = ghρ to P/(gρ) = h and plug the variables into the equation.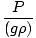 = =  = 10.3 m = 10.3 m |
Problem :
In a fit of inspiration and hot air, you have blown the world's largest balloon. Your two cousins, Bongo the 300 lb. gorilla and Jeeves the 70 lb. weakling, both want to climb to the top of your balloon. When Bongo goes, he goes in style. He wants to lay down on his 1 m by 5 m air bed at the summit. Jeeves proposes to bounce on the top of the balloon on his pogo stick, whose head has an area of 0.001 m2. Assume that the masses of the bed and pogo stick are negligible, and that their occupants' weights are evenly distributed upon them.
You know that your balloon can sustain 200 more kPa of pressure on its surface before it pops. Assuming both can make it to the top without damaging the balloon (or themselves), which cousin(s) should you allow to climb?
P = F/A, so the first thing we need to do is convert everything to the appropriate units. Let's use SI units. 1 lb = 0.454 kg, and F = (mass)×(9.8 m/s2), so Bongo and Jeeves exert forces of 1330 and 311 Newtons, respectively. P = F/A, so Bongo has a pressure of PBongo = = 270 Pa. Jeeves
exerts a pressure of PJeeves = (311 N)×(0.001 m2) = 310 kPa. You should allow Bongo on, but not Jeeves.
= 270 Pa. Jeeves
exerts a pressure of PJeeves = (311 N)×(0.001 m2) = 310 kPa. You should allow Bongo on, but not Jeeves.
Problem :
After an interdimensional mishap, Blaise finds himself on a strange planet with
nothing but an empty barometer and a jar of alien liquid. After working with
barometers for many years, Blaise has developed a keen sense of pressure. He
reckons that the atmospheric pressure is 1.4 atmospheres. The label on
the jar claims that the density of the liquid is 1.0×105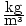 . He pours the liquid into his barometer, and
finds that the atmosphere supports a column 0.072 m tall. What is the
gravitational acceleration g on this planet?
. He pours the liquid into his barometer, and
finds that the atmosphere supports a column 0.072 m tall. What is the
gravitational acceleration g on this planet?
 = g = g |
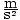 .
.
Please wait while we process your payment





