Previous Next

Properties of Logarithms

Logarithms have the following properties:

Since a0 = 1 and a1 = a:

Property A: loga1 = 0
Property B: logaa = 1
Since ax and logax are inverses:
Property C: logaax = x
Property D: alogax = x
Since apaq = ap+q and 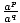= ap-q:
Property E: loga(pq) = logap + logaq
Property F: loga(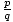) = logap - logaq
Since loga(Mn) = loga(M·M·M ... M) = logaM + logaM + logaM + ... + logaM = n·logaM
Property G: loga(Mn) = n·logaM

Property H

Logarithms have an additional property, called property H, and a property H1 that is a specific case of property H.

Property H: logaM = 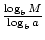, where b is any base.
Property H1: logaM =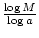

Applications of Properties

The numerous properties listed on this page can be used to evaluate logarithmic functions. Property H1 is especially useful when evaluating logarithms with a calculator: since most calculators only evaluate logarithms with base 10, we can evaluate logaM by evaluating 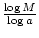. For example, log34 = .


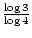Example:

log510 + log520 - log58 =?


 =log5()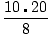  
 =log525  
 =log552  
 =2.  

Previous section Next section

Take a Study Break