Previous Next

Solving Equations Containing Variable Exponents

To solve an equation containing a variable exponent, isolate the exponential quantity. Then take a logarithm, to the base of the exponent, of both sides.


Example 1: Solve for x: 3x = 15.

3x = 15
log33x = log315
x = log315
x =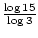
x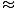 2.465


Example 2: Solve for x: 4·52x = 64.

4·52x = 64
52x = 16
log552x = log516
2x = log516
2x =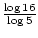
2x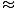 1.723
x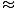 0.861

Solving Equations Containing Logarithms

To solve an equation containing a logarithm, use the properties of logarithms to combine the logarithmic expressions into one expression. Then convert to exponential form and evaluate. Check the solution(s) and eliminate any extraneous solutions--recall that we cannot take the logarithm of a negative number.

Example 1: Solve for x: log3(3x) + log3(x - 2) = 2.

log3(3x) + log3(x - 2) = 2
log3(3x(x - 2)) = 2
32 = 3x(x - 2)
9 = 3x2 - 6x
3x2 - 6x - 9 = 0
3(x2 - 2x - 3) = 0
3(x - 3)(x + 1) = 0
x = 3, - 1
Check:

  • x = 3: log3(3·3) + log31 = 2 + 0 = 2. x = 3 is a solution.
  • x = - 1: log3(3· -1) + log3(- 1 - 2) = log3(- 3) + log3(- 3) does not exist. x = - 1 is not a solution.
Thus, x = 3.


Example 2: Solve for x: 2 log(2x+1)(2x + 4) - log(2x+1)4 = 2.

2 log(2x+1)(2x + 4) - log(2x+1)4 = 2
log(2x+1)(2x + 4)2 - log(2x+1)4 = 2
log(2x+1)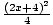 = 2
(2x + 1)2 =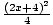
(2x + 1)2 =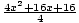
4x2 +4x + 1 = x2 + 4x + 4
3x2 - 3 = 0
3(x2 - 1) = 0
3(x + 1)(x - 1) = 1
x = 1, - 1
Check:

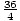  • x = 1: 2 log36 - log34 = log362 - log34 = log3 = log39 = 2. x = 1 is a solution.
  • x = - 1: 2 log-12 - log-14 does not exist (the base cannot be negative).
Thus, x = 1.

Previous section Next section

Take a Study Break