Logarithmic Functions

Solving Exponential and Logarithmic Equations

Solving Equations Containing Variable Exponents

To solve an equation containing a variable exponent, isolate the exponential quantity. Then take a logarithm, to the base of the exponent, of both sides.

Example 1: Solve for x : 3^x = 15 .

3^x = 15
log₃3^x = log₃15
x = log₃15
x =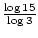
x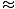 2.465

Example 2: Solve for x : 4·5^2x = 64 .

4·5^2x = 64
5^2x = 16
log₅5^2x = log₅16
2x = log₅16
2x =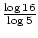
2x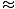 1.723
x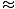 0.861

Solving Equations Containing Logarithms

To solve an equation containing a logarithm, use the properties of logarithms to combine the logarithmic expressions into one expression. Then convert to exponential form and evaluate. Check the solution(s) and eliminate any extraneous solutions--recall that we cannot take the logarithm of a negative number.

Example 1: Solve for x : log₃(3x) + log₃(x - 2) = 2 .

log₃(3x) + log₃(x - 2) = 2
log₃(3x(x - 2)) = 2
3² = 3x(x - 2)
9 = 3x ² - 6x
3x ² - 6x - 9 = 0
3(x ² - 2x - 3) = 0
3(x - 3)(x + 1) = 0
x = 3, - 1
Check:

• x = 3 : log₃(3·3) + log₃1 = 2 + 0 = 2 . x = 3 is a solution.
  
• x = - 1 : log₃(3· -1) + log₃(- 1 - 2) = log₃(- 3) + log₃(- 3) does not exist. x = - 1 is not a solution.
  

Thus, x = 3 .

Example 2: Solve for x : 2 log_(2x+1)(2x + 4) - log_(2x+1)4 = 2 .

2 log_(2x+1)(2x + 4) - log_(2x+1)4 = 2
log_(2x+1)(2x + 4)² - log_(2x+1)4 = 2
log_(2x+1)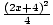 = 2
(2x + 1)² =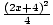
(2x + 1)² =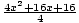
4x ² +4x + 1 = x ² + 4x + 4
3x ² - 3 = 0
3(x ² - 1) = 0
3(x + 1)(x - 1) = 1
x = 1, - 1
Check:

• x = 1 : 2 log₃6 - log₃4 = log₃6² - log₃4 = log₃ = log₃9 = 2 . x = 1 is a solution.
  
• x = - 1 : 2 log_-12 - log_-14 does not exist (the base cannot be negative).

Thus, x = 1 .