| f (x) = a0 + a1x + a2x2 + ....an-1xn-1 + anxn |
where a0, a1, a2,...an are constants and n is a nonnegative integer. n denotes the "degree" of the polynomial.
You should be familiar with the common names of certain polynomial functions. A second-degree polynomial function is a quadratic function (f (x) = ax2 + bx + c). A first-degree polynomial function is a linear function (f (x) = ax + b). Finally, a zero-degree polynomial function is a simply a constant function (f (x) = c).
Rational Functions
A rational function is a function r of the form
r(x) = 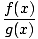 |
where f (x) and g(x) are both polynomial functions. For example,
r(x) = 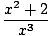 |
is a rational function. Note that we must exclude from the domain of r(x) any value of x that would make the denominator, g(x) equal zero, since this would make r(x) undefined. Thus, x = 0 is not in the domain of the function r(x) we just defined above.
Even and Odd Functions
Another useful classification of functions is even and odd. For an even function, f (- x) = f (x) for all x in the domain. This sort of function is symmetric with respect to the y-axis. For example:
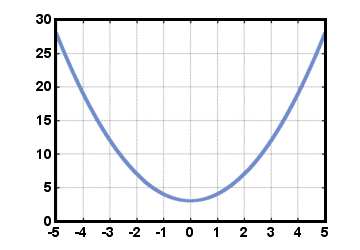
For an odd function, f (- x) = - f (x) for all x in the domain. This sort of function is symmetric with respect to the origin. For example:
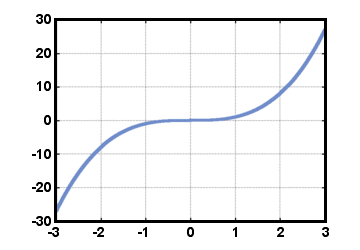
Composite Functions
As we know, f is a function that can take an input x and transform it into an output
f (x). Similarly, f can take the output of another function, such as g(x) as
its input, and transform that input into f (g(x)). When two functions are combined so
that the output of one function becomes the input for the other, the resulting combined
function is called a composite function.
The notation for the composite function f (g(x)) is (fog)(x).
Example:
If f (x) = 3x + 4 and g(x) = 2x - 7, then how could we find (fog)(2)?
Solution:
The problem is asking us to find f (g(2)). One way is to work step-by-step with g and then with f:
g(2)
= 2(2) - 7
= -3
Now we use g(2) = - 3 as the input for f:
f (g(2))
= f (- 3)
= 3(- 3) + 4
= -5
A second way would be to solve for (fog)(x)
directly.
f (g(x))
= f (2x - 7)
= 3(2x - 7) + 4
= 6x - 21 + 4
= 6x - 17
Now, we can plug x = 2 into this function: f (g(2)) = 6(2) - 17 = - 5
Piecewise-Defined Functions
One type of function we'll be dealing with often in calculus is the piecewise-defined function. These functions are defined differently for different intervals in their domain. For example, consider the following piecewise function:
f (x) = 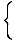 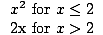 |
For x less than or equal to 2, f (x) is defined by f (x) = x2. For x greater than 2, f (x) is defined by f (x) = 2x. Thus, f (1) = 12 = 1, and f (4) = 2(4) = 8. The graph of this function is below:
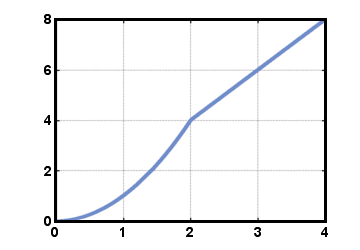
Interval Notation
Finally, we should briefly mention interval notation, which we'll be using throughout the rest of the guide. An interval is a set of all numbers between two endpoints. An closed interval includes both of the endpoints, while an open interval includes neither of the endpoints. So, [a, b] means the set of all x such that a≤x≤b (closed interval) (a, b) means the set of all x such that a < x < b (open interval) Intervals can also be half-open (and half-closed). For example, [a, b) is closed at x = a and open at x = b. This interval represents a≤x < b Intervals that have infinity as an endpoint should always be open at infinity, since no interval can actually contain infinity. Thus, "all numbers less than 4" should be written as (- ∞, 4] , while "the set of all real numbers" should be written as (- ∞,∞).


 payment page
payment page



