Introduction to Integrals

Antiderivatives

An antiderivative of a function f is a function whose derivative is f . In other words, F is an antiderivative of f if F' = f . To find an antiderivative for a function f , we can often reverse the process of differentiation.

For example, if f = x ⁴ , then an antiderivative of f is F = 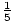x ⁵ , which can be found by reversing the power rule. Notice that not only is 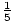x ⁵ an antiderivative of f , but so are 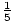x ⁵ + 4 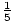, x ⁵ + 6 , etc. In fact, adding or subtracting any constant would be acceptable.

This should make sense algebraically, since the process of taking the derivative (i.e. going from F to f ) eliminates the constant term of F .

Because a single continuous function has infinitely many antiderivatives, we do not refer to "the antiderivative", but rather, a "family" of antiderivatives, each of which differs by a constant. So, if F is an antiderivative of f , then G = F + c is also an antiderivative of f , and F and G are in the same family of antiderivatives.

Indefinite Integral

The notation used to refer to antiderivatives is the indefinite integral. f (x)dx means the antiderivative of f with respect to x . If F is an antiderivative of f , we can write f (x)dx = F + c . In this context, c is called the constant of integration.

To find antiderivatives of basic functions, the following rules can be used:

1. x ⁿ dx = 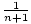x ⁿ⁺¹ + c as long as n does not equal -1. This is essentially the power rule for derivatives in reverse
2. cf (x)dx = c f (x)dx . That is, a scalar can be pulled out of the integral.
3. (f (x) + g(x))dx = f (x)dx + g(x)dx . The antiderivative of a sum is the sum of the antiderivatives.
4. sin(x)dx = - cos(x) + c
   cos(x)dx = sin(x) + c
   sec²(x)dx = tan(x) + c
   These are the opposite of the trigonometric derivatives.