Previous Next

u-Substitution

Sometimes, it is impossible to find the integral of a function using the methods already discussed. The method of u-substitution allows for the integration of more complex functions, and is essentially a form of the chain-rule in reverse.

The general idea is to change a complex integral involving the variable x and dx into a simpler integral involving the variable u and du. The simpler integral can be evaluated, and then the relation between u and x can be used to express the result in terms of x.


Example: Find (4x - 2)3dx

This indefinite integral cannot be evaluated directly by the methods already presented. The first step of a u-substitution is to pick an appropriate part of the original function to be equal to u. This step is often a matter of trial and error. In this case, however, the choice seems obvious. Let u = 4x - 2. Now, to find the relationship between du and dx, take the derivative of u with respect to x:

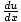= 4
Rearranging, this means that du = 4dx, or dx = 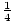du.

With this information, we can substitute u and du into the original integral:

(4x - 2)3dx = (u)3()du    

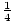
To evaluate this integral, the constant can first be pulled out: =u3du. By basic integration rules, this is equal to 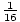u4. Now, this result should be translated back into a function of the variable x by using the relation u = 4x - 2. Substituting x back into the formula yields:

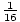(4x - 2)4

Previous section Next page Methods of Calculating Integrals page 2

Take a Study Break