Problem :
Suppose a rock is thrown straight up from atop a 200-meter-high cliff at an initial
speed of 30 feet per second. The height, in meters, of the rock above the ground (until
it lands) at time t is given by the function h(t) = - gt2/2 + 30t + 200, where g 9.81 is a constant of gravitational acceleration. When does the rock reach its maximum
height? What is this maximum height? How fast is the rock moving after 3 seconds?
9.81 is a constant of gravitational acceleration. When does the rock reach its maximum
height? What is this maximum height? How fast is the rock moving after 3 seconds?
When the rock reaches its maximum height, it is instantaneously stationary, with speed
0. Solving
for
t, we obtain
t = 30/g 3.06
3.06 as the time when the rock reaches its maximum
height. Substituting back into
h(t), we find that the maximum height is
h(30/g) = 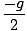 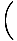 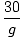  +30 +30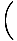 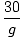 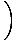 +200 = +200 =  +200 +200  245.89 245.89 |
|
measured in meters. To find the speed at time
t = 3, we compute
h'(3) = (- g)(3) + 30  0.58 0.58 |
|
meters per second, which makes sense, because the rock is about
0.06 seconds away from
reaching its maximum height and coming to an instantaneous stop.
Problem :
The position of a box, in a certain coordinate system, attached to the end of a spring is given by p(t) = sin(2t). What is the acceleration of the box at time t? How does this relate to its position?
The velocity of the box is equal to
and the acceleration is given by
| p''(t) = - 4 sin(2t) = - 4p(t) |
|
This makes sense, because the spring should exert a restoring force proportional to the
displacement of the box and in the opposite direction from the displacement.
Problem :
Suppose the velocity of a sprinter (in meters per second) at time t seconds after the start of a 40 meter dash is given by
How fast is the sprinter accelerating
1 second after she starts sprinting?
The acceleration is given by
v'(t) = 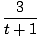 |
|
at time
t. Thus the acceleration at time
t = 1 is
3/2 meters per second per second.