Calculus BC: Applications of the Derivative
Optimization
Optimization is nothing more than finding the minimum or maximum values of a function within a specified part of its domain. For instance, a function f (x) may represent a quantity of practical significance (profit, revenue, temperature, efficiency) with the variable x representing a quantity that can be controlled (expenditures, investment, throttle, length of work day). Then an approximate formula for f (x) , for instance f (x) = x 2 - 3x , might make sense for values of x that have no real significance (such as negative length), so the domain of f must be artificially restricted to fit with the practical application.
To find the global maximum or minimum of f , if it exists, one must check determine the positions of the local maxima and local minima, and compare these to the values of f at the endpoints of its domain, if there are any.
It may happen that a function, such as
f (x) = x
3
with domain
[3, 4]
, does not have any
critical points, but attains a global maximum at an endpoint -- in this case
f (4) = 64
. It
may also happen that a function has critical points but does not have a global maximum or
minimum, for instance
f (x) =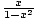 
with domain
(- 1, 1)
. The latter phenomenon
uses the "openness" of the domain
(- 1, 1)
in an essential way; the function has no maximum
or minimum exactly because it approaches
±∞
at the omitted endpoints
±1
.
The most convenient setting for optimization problems is then a differentiable function f whose domain is a closed interval [a, b] . In this case, f has both a global maximum and a global minimum, each of which is either a critical point or a boundary point (i.e. (a, f (a)) and (b, f (b)) ).
