Calculus BC: Applications of the Derivative
Related Rates
In many practical situations, two quantities that change over time are related directly by an equation. The method of related rates enables us to calculate the rate at which one quantity is changing when the rate of change of the other quantity is given.
For example, suppose as before a gigantic ice-cream cone (with sides at 30 o from the vertical) is being filled with water at a constant rate of 2 cubic feet per second. Suppose further that we want to calculate the rate at which the water level in the cone is rising when it is 5 feet from the bottom of the cone.
Let h(t) be the height in feet of the water level above the bottom of the cone at time t , measure in seconds. Let V(t) be the volume, in cubic feet, of water in the cone at time t . Since the sides of the cone are 30 o from vertical, the radius of the cone at height h is equal to sin(30 o )h = h/2 . It follows from basic geometry that
| V(t) | = |
Π
h(t)
h(t) |
|
| = |
h(t)3
|
Differentiating both sides with respect to t (using the chain rule), we have
 (t) = (3h(t)2) (t) = 
(t)
|
We are given that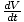
(t) = 2
; using this and setting
h(t) = 5
, we solve for
(t)
:
(t) = 
(t) =  (2) = 
|
The related rates method illustrated above can be applied in a variety of contexts. Each time, the basic method is the same:
- Determine the two relevant quantities.
- Write down the relation between them.
- Differentiate both sides of the relation with respect to t .
- Solve for the rate or quantity of interest in terms of other rates and quantities.
- Use initial conditions to determine the rates and quantities to substitute into the formula from (4).
