There is an easy way to write down a linear function whose graph passes through two given points with different x-coordinates. If (x1, y1) and (x2, y2) are two points, the line through them has equation (x2 - x1)(y - y1) = (y2 - y1)(x - x1). If x1≠x2, we may divide through by (x2 - x1) and add y1 to each side to get the function:
f (x) = y = 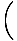 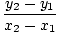 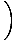 (x - x1) + y1 (x - x1) + y1 |
This can be expanded into the standard form for linear functions, and doing so we find
the slope to be  and the y-intercept
and the y-intercept 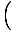 y1 -
y1 - 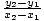 x1
x1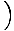 .
.
Linear functions are associated with constant rates of change. For example, suppose you are pouring iced tea into a glass at a constant rate of 50 milliliters per second. If the glass contains 65 milliliters of iced tea at time t = 0 (where t is measured in seconds), then the number of milliliters of tea in the glass at time t is equal to f (t) = 50x + 65. The slope of the function f is equal to 50 and the y-intercept is equal to 65.
Polynomial Functions
Linear functions are a special case of a more general class of functions called the polynomial functions. A polynomial (of degree n) is an expression of the form anxn + ... + a1x + a0, for some integer n, where an,…, a1, a0 are real numbers with an≠ 0. (The function f (x) = 0, with all ai = 0, is also a polynomial, called the zero polynomial). A polynomial in the form above gives rise to a polynomial function f (x) = anxn + ... + a1x + a0. As an example, consider the function f (x) = x3 +4x2 - 4, plotted below for -4.2≤x≤1.5. Here, ai = 0 for i≥4, a3 = 1, a2 = 4, a1 = 0, and a0 = - 4.
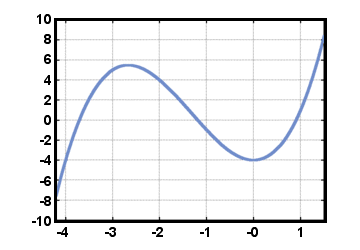
We immediately see, by the horizontal line test, that this function f is not invertible.
Polynomial functions arise in many physical situations. Suppose I drop a bowling ball off the top of a 300-foot tall building. Then according to the principles of Newtonian mechanics, the height (in feet) of the bowling ball above ground, at time t seconds after the ball is dropped, is given by h(t) = - g/2t2 + 300, where g is a constant of acceleration (due to gravity). In order to find out when the bowling ball hits the ground, we could solve the equation h(t) = 0 for t.
Rational Functions
Rational functions are the functions obtained by taking the quotient of one polynomial by another polynomial. A general rational function is therefore given by
f (x) = 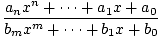 , , |
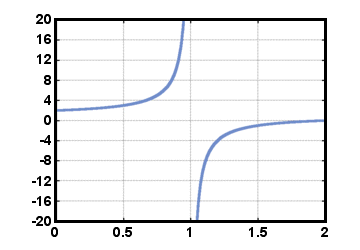
where the polynomial in the denominator must not be identically zero. Note that all polynomial functions are also rational functions. Because the denominator may equal 0 for certain values of x, the domain of a rational function f is not the entire set of real numbers. An example of a rational function is f (x) = (x - 2)/(x - 1), shown below for 0≤x≤2. Note that this function is defined for all real numbers x except for x = 1.
Power Functions
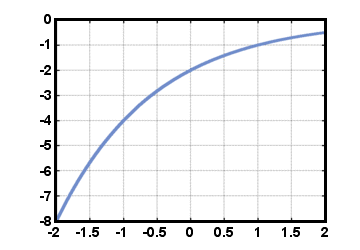
Power functions are functions of the form f (t) = Crt, where C and r are real numbers. The number C is called the initial value, and is equal to the value of the function f (t) at t = 0. The number r is called the growth rate, the amount by which the value of f is multiplied for each increase of 1 in the value of t. Recall some properties of exponents: r0 = 1 for any r≠ 0, and rarb = ra+b for any real number r. A special power function is the exponential function f (t) = et, where e is a constant approximately equal to 2.71828. Such functions often arise in calculating compound interest, and in many natural phenomena. We will see another reason later on for why the number e is so special. The power function f (t) = - 2(1/2)t is shown below for -2≤t≤2.
By the horizontal line test, power functions (with t≠ 0) are invertible. Note, however, that power functions take values only in either the positive or negative real numbers (but not both), so the inverse function will not be defined for all real numbers. Since the inverse function is not among the functions we have introduced so far, we give it a new name. We define the logarithm function g(x) = logr(x) (with the base r) to be the inverse function of f (x) = rx. Then if y = f (x) = rx, we have x = g(y) = logr(y). The inverse functions of all power functions can be expressed in terms of these logarithm functions.
Suppose there are 10 college students at a party at time t = 0 and the number of students at the party doubles every hour. Then the number of students at the party t hours after it starts is given by the function s(t) = 10*2t.
Trigonometric Functions
Though one first learns about the trigonometric functions while studying triangles, perhaps the easiest way to define them is with a circle. We define the cosine of a real number t, cos(t), to be the x-coordinate of the point on the unit circle that is t radians counterclockwise from the positive x-axis. Similarly, the sine of t, sin(t), is defined to be the y-coordinate of the same point. The tangent of t is defined by taking a quotient of these two functions: tan(t) = sin(t)/cos(t). The graphs of the sine and cosine functions behave in a periodic, wave-like, manner, since in traveling around the unit circle, one eventually arrives back at the place where one started. The graph of f (t) = sin(t) is displayed below for -2Π≤t≤2Π.
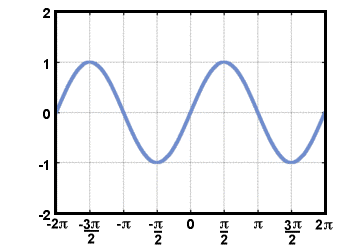
Note that since the definition of the tangent function includes dividing by cos(t), it is not defined when cos(t) = 0. The graph of g(t) = tan(t) is shown below for -2Π≤t≤2Π.
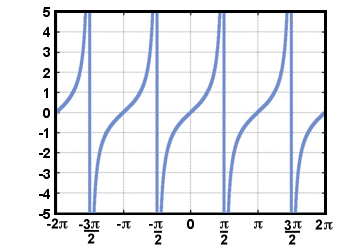
If we want to find inverses for the trigonometric functions, we must restrict their domains so that they will pass the horizontal line test. Customarily, the domain of the sine and tangent functions is restricted to - Π/2≤t≤Π/2 and that of the cosine function to 0≤t≤Π. The inverse functions for the sine and cosine will then have domain -1≤t≤1. We write the inverse functions of sine, cosine, and tangent as sin-1(t), cos-1(t), and tan-1(t), respectively.
Trigonometric functions arise in many periodic physical phenomena, such as tides, times of sunrise, and the motion of a pendulum or a mass on the end of a spring.


 payment page
payment page



