The Derivative
The Derivative Function
Since the derivative of a function
f
at any value
x
0
where the function is
differentiable is just a number,
f'(x
0)
, we may define the derivative function,
denoted
f'(x)
or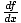
(x)
, to be the function that maps a value
x
where
f
is differentiable to the derivative of
f
at
x
. Since
f'
is a function in
its own right, we can graph it, just like any other function.
For example, let us calculate the derivative function (also called simply the "derivative") of f (x) = 5x . Since the graph of this function is a line with slope 5 , we might guess that the derivative will equal 5 at every point. We verify this with the formula for the derivative of f at a point x :
| f'(x) | = |
|
|
| = |
|
||
| = | 5 |
Indeed, f'(x) = 5 , a constant function.
