payment page
-
Derivative
The instantaneous rate of change of a function f (x) at a particular point x0, denoted f'(x0) or
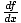(x0). The formal definition is the following limit:
f'(x0) =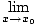 
-
Derivative Function
A function f'(x) taking on the value of the derivative of f (x) at each number x.
-
Difference Quotient
For a function f, and any two points x0 and x in its domain, the quotient:
-
Differentiable
A function f is differentiable at a point (x0) if it has a well-defined derivative at that point. It is simply differentiable if it is differentiable at every point in its domain.
-
Secant Line
A line through two distinct points on the graph of a function.
-
Tangent Line
A line through a point (x, f (x)) on a graph that has slope equal to the derivative of the function f at x. A limit of secant lines to the graph of a function as two contact points approach one another.
