Terms
Cross-Sectional Area Method
-
If
A(x) is the cross-sectional area of a region perpendicular to a
fixed axis at position
x, defined between
x = a and
x = b, then the
total volume of the region is
Vol = 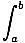 A(x)dx |
|
Disk Method
-
The volume of the region obtained by rotating the area under the graph
of a function
f (x) between
x = a and
x = b about the
x-axis is
equal to
| Vol = 2Π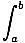f (x)2dx |
|
This is an application of the cross-sectional area method, noting
that that cross section to this surface of revolution perpendicular to
the
x-axis is a circle of radius
f (x).
Shell Method
-
The volume of the region obtained by rotating the area under a
function
f (x) between
x = a and
x = b about the
y-axis is equal
to:
| Vol = 2Π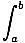xf (x)dx |
|
Solid of Revolution
-
The solid swept out by a region in the plane when rotated about an
axis. Examples include cylinders, cones, and spheres (all considered
as solids with their interiors). The volume of such a region can be
computed via the disk method or the shell method.
Surface of Revolution
-
The surface swept out by a curve in the plane when rotated about an
axis. Examples include the surface of a cylinder, cone, or sphere,
and more generally the surface of any solid of revolution.
