Problem :
Find all roots, real and complex, of the following polynomial: x2 + 4.
x = {2ı, -2ı}.
Problem :
Find all roots, real and complex, of the following polynomial: x4 - x3 - x2 - x - 2.
x = {2, -1,ı, - ı}
Problem :
If 3ı is a root of a polynomial, what must one other root be?
The complex conjugate of
3ı must be a root also, so
-3ı is
also a root of the polynomial.
Problem :
Find all roots, real and complex, of the following polynomial: x3 +4x2 + 25x + 100.
x = { -4, 5ı, -5ı}.
Problem :
Find all roots, real and complex, of the following polynomial: x4 +2x2 - 3.
x = {1, -1,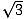 ı, -
ı, - 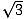 ı}
ı}.
Problem :
Find all roots, real and complex, of the following polynomial: x8 +2x7 +4x6 +8x5 - x4 -2x3 -4x2 - 8x.
x = {0, -2, -1, 1,ı, - ı, 2ı, -2ı}.