Complex Numbers
Operations With Complex Numbers
Two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. For any complex numbers a + bı and c + dı , the following rules are true for the four basic operations.
operations
| (a + bı) + (c + dı) = (a + c) + (b + d )ı |
| (a + bı) - (c + dı) = (a - c) + (b - d )ı |
| (a + bı)×(c + dı) = (ac - bd )+ (ad + bc)ı |
fraca+bıc+dı = 
|
The technique for dividing complex numbers involves multiplying the denominator by its complex conjugate. The complex conjugate of a complex number a + bı is a - bı . Complex conjugates are useful and special for the following reasons:
conjugates
| (a + bı) + (a - bı) = 2a |
| (a + bı) - (a - bı) = 2bı |
| (a + bı)×(a - bı) = a 2 + b 2 |
 = 
|
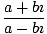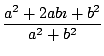When complex conjugates are added or multiplied, the sum or product is real. So when the denominator of a fraction is a complex number, you can multiply the numerator and the denominator by the complex conjugate of the denominator to get a fraction with a real denominator.
The complex conjugate is an important tool for simplifying expressions with complex numbers. Another important fact about complex conjugates is that when a complex number is the root of a polynomial with real coefficients, so is its complex conjugate. We'll take a closer look in the next section.
