The Fundamental Theorem of Algebra states that every polynomial of degree one or
greater has at least one root in the complex number system (keep in mind
that a complex number can be real if the imaginary part of the complex root
is zero). A further theorem, in some cases referred to as the Linear
Factorization Theorem, states that a polynomial of degree n has exactly n
linear factors, and each can be written in the form (x - c), where c is a
root. These n complex roots (possibly including some real roots) are counted
with multiplicity. This much was explained in Roots of Higher Degree
Polynomials.
In Roots of Higher Degree Polynomials, we discussed how a polynomial can be
resolved into linear factors irreducible over the reals. The factors that
are first-degree polynomials are real roots of the original polynomial. The
factors that are second-degree polynomials can't be reduced using real numbers. With
complex numbers, however, we can solve those quadratic equations which are
irreducible over the reals, and we can then find each of the n roots of a
polynomial of degree n.
A given quadratic equation ax2 + bx + c = 0 in which b2 -4ac < 0 has two
complex roots: x =  ,
, . Therefore, whenever a complex number is a root of
a polynomial with real coefficients, its complex conjugate is also a root of
that polynomial.
. Therefore, whenever a complex number is a root of
a polynomial with real coefficients, its complex conjugate is also a root of
that polynomial.
As an example, we'll find the roots of the polynomial x5 - x4 + x3 - x2 - 12x + 12.
complexroots
| x5 - x4 + x3 - x2 - 12x + 12 = 0 |
|
| (x - 1)(x4 + x2 - 12) = 0 |
|
| (x - 1)(x2 -3)(x2 + 4) = 0 |
|
(x - 1)(x + 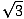 )(x - )(x - 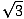 )(x2 + 4) = 0 )(x2 + 4) = 0 |
|
(x - 1)(x + 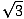 )(x - )(x - 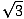 )(x + 2ı)(x - 2ı) = 0 )(x + 2ı)(x - 2ı) = 0 |
|
The fifth-degree polynomial does indeed have five roots; three real, and two
complex.