Limits and Continuity

The concept of the limit is one of the most crucial things to understand in order to prepare for calculus. A limit is a number that a function approaches as the independent variable of the function approaches a given value. For example, given the function f (x) = 3x , you could say, "The limit of f (x) as x approaches 2 is 6 ." Symbolically, this is written 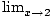f (x) = 6 . In the following sections, we will more carefully define a limit, as well as give examples of limits of functions to help clarify the concept.

Continuity is another far-reaching concept in calculus. A function can either be continuous or discontinuous. One easy way to test for the continuity of a function is to see whether the graph of a function can be traced with a pen without lifting the pen from the paper. For the math that we are doing in precalculus and calculus, a conceptual definition of continuity like this one is probably sufficient, but for higher math, a more technical definition is needed. Using limits, we'll learn a better and far more precise way of defining continuity as well. With an understanding of the concepts of limits and continuity, you are ready for calculus.