More Trigonometric Identities: Double and Half-Angle Formulas

The following identities equate trigonometric functions of double angles to expressions that involve only trigonometric functions of single angles. They are very useful in differentiation and other general simplification.

sin(2x) = 2 sin(x)cos(x)

cos(2x) = cos²(x) - sin²(x) = 1 - 2 sin²(x) = 2 cos²(x) - 1

tan(2x) =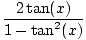

The following identities equate trigonometric functions of half-angles to expressions that involve only trigonometric functions of single angles.

sin

= ±

cos

= ±

tan

= ±

If an angle in question is a variable, these formulas are sometimes the only means by which the trigonometric expression can be simplified. Even when an angle is known, these identities can be useful in simplifying expressions. They should be memorized.

One additional formula is useful in conjunction with triangles. For any triangle ABC, tan(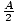) = 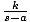where s is the semiperimeter (s = 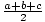) and k = 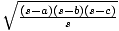. This is another way to express the half-angle formula for tangent.