Previous Next

These formulas are especially helpful when an angle whose function values you haven't memorized can be expressed as the sum or difference of two angles whose function values you have memorized.

The following formulas express the values of trigonometric functions of the sum of angles in terms of sums of the products of functions of single angles.

sin(α + β) = sin(α)cos(β) + cos(α)sin(β)    

cos(α + β) = cos(α)cos(β) - sin(α)sin(β)    

tan(α + β) =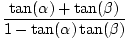    

The following formulas express the values of trigonometric functions of the difference of angles in terms of sums of the products of functions of single angles.

sin(α - β) = sin(α)cos(β) - cos(α)sin(β)    

cos(α - β) = cos(α)cos(β) + sin(α)sin(β)    

tan(α - β) =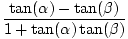    

Previous section Next section

Take a Study Break