Problem : Calculate the eccentricity of an ellipse with one focus at the origin and the other at $(-2k, 0)$, and semimajor axis length $3k$.
It is easiest if we draw a diagram of the situation: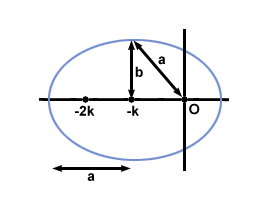
Problem : For an ellipse with its major axis parallel to the $x$-direction and its rightmost focus at the origin, derive the position of the other focus in terms of its eccentricity $\epsilon$ and $k$, where $k$ is defined as $k = a(1- \epsilon^2)$.
The $y$-coodinate of the other focus is the same--zero. The other focus is a distance $2\sqrt{a^2 – b^2}$ in the negative x-direction, so the coordinates are $(-2\sqrt{a^2-b^2},0)$. But $\epsilon = \sqrt{1 - \frac{b^2}{a^2}}$ so we can write $-2\sqrt{a^2-b^2} = -2a\sqrt{1 – \frac{b^2}{a^2}} = -2a\epsilon$. We are given that $k = a(1 - \epsilon^2)$, so $a = \frac{k}{1 - \epsilon^2}$, and $- 2a\epsilon = \frac{-2k\epsilon}{1 – \epsilon^2}$. Thus the coordinate of the other focus is $(\frac{-2k\epsilon}{1\epsilon^2},0)$.Problem : The general equation for orbital motion is given by: \begin{equation} x^2 + y^2 = k^2 – 2k\epsilon x + \epsilon^2 x^2 \end{equation} Where the $k$ is the same $k$ as in the last problem: $k = a(1-\epsilon^2) = \frac{L^2}{GMm^2}$. Show that when $\epsilon = 0$, this reduces to an equation for a circle. What is the radius of this circle?
Clearly, when $\epsilon = 0$ the second and third terms on the right hand side go to zero, leaving: \begin{equation} x^2 + y^2 = k^2 \end{equation} This is the equation for a circle of radius $k$. Since $\epsilon$ is dimensionless and $k = a(1 - \epsilon^2)$, $k$ has the correct units of distance.Problem : Derive the formula for the area of an ellipse by integration.
The equation for an ellipse is given by: \begin{equation} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \end{equation} Solving for $y$ yields, $y = b\sqrt{1 - \frac{x^2}{a^2}}$. We can take an ellipse centered at the origin and look at the area in the first quadrant. Because of symmetry, the total area will be four times this. Thus, \begin{equation} \frac{A}{4} = b\int_0^a \sqrt{1 – \frac{x^2}{a^2}} dx \end{equation} We can trigonometric substitution, $x = a\sin\theta$, then $dx = a\cos\theta d\theta$. The limits of integration can now be chosen as $\theta = 0$ and $\theta = \pi/2$. Then: \begin{equation} \frac{A}{4} = b\int_0^{\pi/2} \sqrt{1 - \sin^2\theta} a\cos\theta d\theta = ab\int_0^{\pi/2} = cos^2\theta d\theta = \frac{\pi ab}{4} \end{equation} So the total area is $A = \pi ab$.Problem : Prove that for a point on an ellipse, the sum of the distances to each foci is a constant.
We can say without loss of generality that the ellipse is centered at the origin and then the coordinates of the foci are $(\pm\sqrt{a^2 – b^2},0)$. Then a point on the ellipse with coordinates $(x,y)$ will be a distance: \begin{equation} ((x-\sqrt{a^2-b^2})^2 + y^2)^{1/2} \end{equation} from one foci and distance: \begin{equation} ((x + sqrt{a^2-b^2})^2 + y^2)^{1/2} \end{equation} from the other focus. Thus the total distance is just the sum: \begin{equation} D= ((x-\sqrt{a^2-b^2})^2 + y^2)^{1/2} + ((x+\sqrt{a^2-b^2})^2 + y^2)^{1/2} \end{equation} But the equation for an ellipse tells us that $y^2 = b^2(1 - \frac{x^2}{a^2})$, and we can substitute this in: \begin{equation} D = ((x-\sqrt{a^2-b^2})^2 + b^2(1 -\frac{x^2}{a^2}))^{1/2} + ((x-\sqrt{a^2-b^2})^2 + b^2(1 -\frac{x^2}{a^2}))^{1/2} \end{equation} We can then square this to find: \begin{equation} D^2 = 2x^2 + 2(a^2 – b^2) +2b^2(1 - \frac{x^2}{a^2}) - 2\sqrt{(x-\sqrt{a^2-b^2})^2 + b^2(1 -\frac{x^2}{a^2}))^2 – 4x^2(a^2-b^2)} \end{equation} Expanding out the terms under the square root we find: \begin{equation} D^2 = 2x^2 + 2a^2 – 2b^2 + 2b^2 - \frac{2b^2x^2}{a^2} – 2x^2 + 2a^2 + \frac{2b^2x^2}{a^2} = 4a^2 \end{equation} Therefore the total distance is independent of the coordinates $x$ and $y$, and is $2a$, as we would expect, since it is obvious that the distance has to be this at the narrow endpoints of the ellipse.












