Kepler's Second Law can be stated in several equivalent ways:

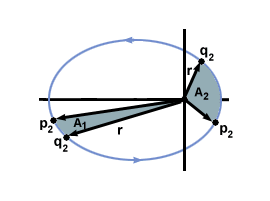
1. If we draw a line from the sun to the planet in question (a radius), then as the planet moves around in its orbit it will sweep out some area A₁ in time t. If we consider the planet elsewhere on its orbit, then over the same time interval t its radius will sweep out another area, A₂. Kepler's Second Law states that A₁ = A₂. This law is often referred to as the "law of equal areas."
2. Alternatively, any two radial lines between the sun and the elliptical orbit of a planet form some area (for convenience let us again call this A₁). The points where these radii intersect the orbit are labeled p₁ and q₁. We then choose two more radial lines that form another area A₂ that is equal in size to A₁ and label the points where these radii intersect p₂ and q₂. Then Kepler's Second Law tells us that the time taken for the planet to pass between points p₁ and q₁ is equal to the time taken to pass between points p₂ and q₂.

Keplers Second Law means that the closer a planet is to the sun, the faster it must be moving on its orbit. When the planet is far away from the sun, it only has to move a relatively small distance in order to sweep out a large area. However, when the planet is close to the sun it must move a lot further in order to sweep out an equal area. This can be seen most clearly in Figure 2.1.

Kepler's Second Law is an example of the principle of conservation of angular momentum for planetary systems. We can make a geometrical argument to show how this works.

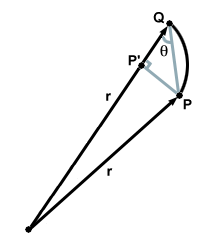
Consider two points P and Q on the orbit of a planet, separated by avery small distance. Suppose that it takes a small time dt for the planet to move from P to Q. Because the line segment is small, we can make the approximation that it is a straight line. Then , being the infinitesimal distance dx over which the planet moved in time dt, represents the average velocity of the planet over that small range. That is = . Now consider the area swept out in this time dt. It is given by the area of the triangle SPQ, which has height PP' and base r. But it is also clear from figure 2.2 that PP' = | PQ| sinθ. Thus the area swept out per time dt is given by:

But Kepler's Second Law asserts that equal areas must be swept out in equal time intervals or, expressed differently, area is swept out at a constant rate (k). Mathematically:

But we just this value:

Angular momentum is given by the expression:

where m is the mass being considered. The magnitude of the angular momentum is clearly mvr sinθ where we are now considering the magnitudes of and . Kepler's Second Law has demonstrated that k = , and thus:

Since the mass of any planet remains constant around the orbit, we have shown that the magnitude of the angular momentum is equal to a constant. Thus Kepler's Second Law demonstrates that angular momentum is conserved for an orbiting planet.