Problem : What is the force exerted by Big Ben on the Empire State building? Assume that Big Ben has a mass of 108 kilograms and the Empire State building 109 kilograms. The distance between them is about 5000 kilometers and Big Ben is due east of the Empire State building.
The direction of the force clearly attracts the Empire State towards Big Ben. So the direction is a vector pointing due east from New York. The magnitude is given by Newton's Law:F = 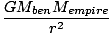 = = 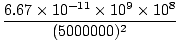 = 2.67×10-7N = 2.67×10-7N |
Clearly, the gravitational force is negligibly small, even for quite large objects.
Problem : What is the gravitational force that the sun exerts on the earth? The earth on the sun? In what direction do these act? (Me = 5.98×1024 and Ms = 1.99×1030 and the earth-sun distance is 150×109 meters).
First, consider the directions. The force acts along the direction such that it attracts each body radially along a line towards their common center of mass. For most practical purposes, this means a line connecting the center of the sun to the center of the earth. The magnitude of both forces is the same, as we would expect from Newton's Third Law, and they act in opposite directions, both attracting each other mutually. The magnitude is given by:F = 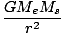 = = 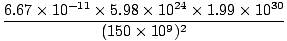 = 3.53×1022 = 3.53×1022 |
Problem :
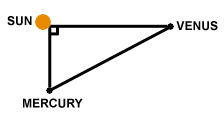
Fs = 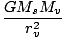 = 5.54×1022 = 5.54×1022 |
The distance between Mercury and Venus is given by rmv =
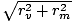 = 1.08×1011
meters. The magnitude of the force from Mercury, then, is:
= 1.08×1011
meters. The magnitude of the force from Mercury, then, is:
Fm = 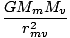 = 9.19×1015 = 9.19×1015 |
The directions of these forces are along the lines connecting the planets. If the size of the forces was comparable, we would have to resolve each vector force into components perpendicular and parallel to some direction, and then sum these components in order to find the final direction of the force. In this case however, the force due to the sun is more than a million times greater than the force due to Mercury, and so the net force is very well approximated by the magnitude and direction of the force due to the sun.
Problem : It is possible to simulate "weightless" conditions by flying a plane in an arc such that the centripetal acceleration exactly cancels the acceleration due to gravity. Such a plane was used by NASA when training astronauts. What would be the required speed at the top of an arc of radius 1000 metres?
We require an acceleration that exactly cancels that due to gravity -- that is, exactly 9.8 m/sec2. Centripetal acceleration is given by ac =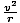 .
We have been given r = 1000 meters, so v =
.
We have been given r = 1000 meters, so v = 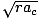 =
= 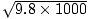
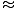 99 m/s.
99 m/s.
Problem : Show using Newton's Universal Law of Gravitation that the period of orbit of a binary star system is given by:
T2 = 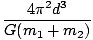 |
Where m1 and m2 are the masses of the respective stars and d is the distance between them. Notice that we derived the same result in a problem in the previous section, using the reduced mass and Kepler's Third Law. Consider the center of mass of the binary star system to be at the origin. Since the planets must be on opposite sides of their center of mass, it must be true that m1r1 - m2r2 = 0 where r1 and r2 are the radii of orbit. Since r2 + r1 = dâá’r2 = d - r1, we can write m1r1 = m2r2 = m2(d - r1). Rearranging, we can solve for r1: r1 =
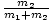 d.
Now the force acting between the two masses is given by Newton's Law:
d.
Now the force acting between the two masses is given by Newton's Law:
F = 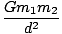 |
We can proceed as we did in deriving Kepler's Third Law from Newton's Law, and say that this force must be equal to the centripetal force acting on m1:
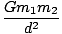 = = 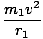 = = 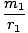 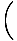 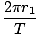  |
Rearranging and then substituting the expression we found for r1, we have:
T2 = 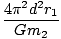 = = 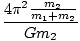 d3 = d3 = 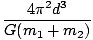 |
Which is the same result we derived from Kepler's Third Law.


 payment page
payment page



