Gravitating Spheres
While exploring Netwon's gravitational discoveries, we calculated g using the fact that the distance between the mass m and the earth was the radius of the earth. In other words, we assumed that all the mass of the earth is concentrated at its center. This supposition may seem reasonable when we are far away from the earth (that is we are at such a distance that the radius of the earth is negligible in comparison), but it doesn't seem so good at all when we are at the earth's surface. However, we will see that this assumption does hold exactly for any body outside the surface of a gravitating sphere (to which the earth is a good approximation). This is a profound result. It is a consequence of superposition, the inverse square law, and the symmetry of a sphere.
The following theorem was proved by Newton in the Principia:
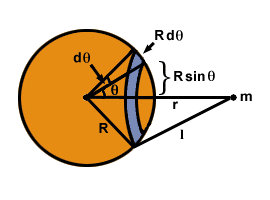
A spherical mass can be thought of as built up of many infinitely thin spherical shells, each one nested inside the other.We will consider the gravitational attraction that such a shell exerts on a particle of mass m, a distance r from the center of the shell. The total mass of the shell is M and its radius is R.
 and
summing over all the masses.
and
summing over all the masses.
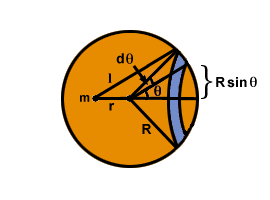
To do this, consider cutting the shell into rings as shown in . Every point on the ring is a distance l from m, and the ring has width Rdθ and radius R sinθ. The surface area of the ring equals 2Π× the area × the width = 2ΠR2sinθdθ. The total mass of the shell, M, is evenly distributed over the surface, so the mass of the ring is given by the fraction of the total surface area (4ΠR2):
Mi = M×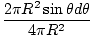 = = 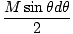 |
For infinitely thin rings, we can take the integral to find the total potential:
U = - 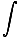 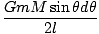 |
But applying the law of cosines to the triangle with sides R, r, and l in we find l2 = R2 + r2±2rR cosθ and taking the differential of both sides: 2ldl = 2rR sinθdθ. This last expression implies that:
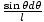 =
= 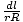 . We can
now rewrite our integral as:
. We can
now rewrite our integral as:
U = - 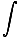 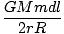 = = 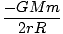  dl dl |
For the ring closest to m, the value of l is r - R and for the ring farthest from m it is R + r. So we can now perform the integral:
U = 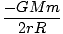 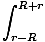 dl = dl =  (2R) = (2R) = 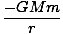 |
This result mirrors the result we would receive if all the mass had been concentrated at the center of the shell. This similarity holds true for all shells, and since a sphere is composed of such shells, it must be true for a sphere too. The phenomenon holds even if the different shells are not of equal mass density--that is, if the density is a function of the radius. We can conclude that the gravitational force exerted by one planet on another acts as if all the mass of each planet were concentrated at its center.
Mass within a gravitating shell
Now let us consider the potential for a particle inside such a shell.
U = 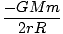 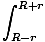 dl = dl = 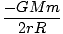 (2r) = (2r) = 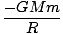 |
Thus the potential inside the sphere is independent of position--that is it is constant in r. Since F =
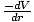 we can infer that
the shell exerts no force on the particle inside it. For a
solid sphere this means that for a particle, the only gravitational
force it feels will be due to the matter closer to center of the sphere
(below it). The matter above it (since it is inside its shell) exerts
no influence on it. clearly illustrates this fact.
we can infer that
the shell exerts no force on the particle inside it. For a
solid sphere this means that for a particle, the only gravitational
force it feels will be due to the matter closer to center of the sphere
(below it). The matter above it (since it is inside its shell) exerts
no influence on it. clearly illustrates this fact.



 payment page
payment page



