Problem :
Two balls with equal masses, m, and equal speed, v, engage in a head on elastic collision. What is the final velocity of each ball, in terms of m and v?
Though we could go through the formal application of the equations of linear momentum, it is easier to think about this problem conceptually. Since the balls of equal mass are moving at equal and opposite speeds, the total linear momentum of the system is zero. For linear momentum to be conserved after the collision, both balls must rebound with the same velocity. If one ball had more speed than the other, there would be a net linear momentum and our conservation principle would be invalid. Having established that both balls rebound with the same speed, we must find what that speed is. Since the collision is elastic, kinetic energy must be conserved. If the final velocity of each ball were more, or less, than its initial velocity, kinetic energy would not be conserved. Thus we can state that the final velocity of each ball is equal in magnitude and opposite in direction to their respective initial velocities.
Problem :
Two balls, each with mass 2 kg, and velocities of 2 m/s and 3 m/s collide head on. Their final velocities are 2 m/s and 1 m/s, respectively. Is this collision elastic or inelastic?
To check for elasticity, we need to calculate the kinetic energy both before and
after the collision. Before the collision, the kinetic energy is
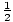 (2)(2)2 +
(2)(2)2 + 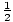 (2)(3)2 = 13. After, the kinetic energy is
(2)(3)2 = 13. After, the kinetic energy is
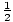 (2)(2)2 +
(2)(2)2 + 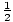 (2)(1)2 = 5. Since the kinetic energies are not
equal, the collision is inelastic.
(2)(1)2 = 5. Since the kinetic energies are not
equal, the collision is inelastic.
Problem :
Two balls of mass m1 and m2, with velocities v1 and v2 collide head on. Is there any way for both balls to have zero velocity after the collision? If so, find the conditions under which this can occur.
First of all, the collision must be inelastic, as the final kinetic energy must be zero, clearly less than the initial kinetic energy. Secondly, we can state that the collision is completely inelastic, as both objects with zero velocity must remain at the site of the collision, i.e., they must stick together. The final principle we must check is that momentum is conserved. Clearly the final momentum of the system must be zero, as neither ball is moving. Thus the same value must be true before the collision. For this to happen, both masses must have equal and opposite momentum, or m1v1 = m2v2. Thus, in a completely inelastic collision in which m1v1 = m2v2, both masses will be stationary after the collision.
Problem :
A car of 500 kg, traveling at 30 m/s rear ends another car of 600 kg, traveling at 20 m/s. in the same direction The collision is great enough that the two cars stick together after they collide. How fast will both cars be going after the collision?
This is an example of a completely inelastic collision. Since the two cars stick together, they must move with a common velocity after the collision. Thus simply using the conservation of momentum is enough to solve for our one unknown variable, the velocity of the two cars after the collision. Relating the initial and final moments:
| po | = | pf | |
| m1v1 + m2v2 | = | Mvf | |
| (500)(30) + (600)(20) | = | (1100)vf | |
| vf | = | 24.5m/s |
Thus both cars will travel at 24.5 m/s, in the same direction as their initial travel.
Problem :
One pool ball traveling with a velocity of 5 m/s hits another ball of the same mass, which is stationary. The collision is head on and elastic. Find the final velocities of both balls.
Here we use our two conservation laws to find both final velocities. Let's call the pool ball that is initially moving ball 1, and the stationary one ball 2. Relating the kinetic energies before and after the collision,
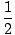 mv1o2 + mv1o2 + 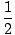 mv2o2 mv2o2 | = | 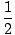 mv1f2 + mv1f2 + 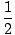 mv2f2 mv2f2 | |
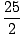 m m | = | 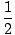 mv1f2 + mv1f2 + 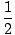 mv2f2 mv2f2 | |
| Canceling the fractions and masses, | |||
| 25 | = | v1f2 + v2f2 |
We also know that momentum must be conserved. The initial momentum is provided entirely by ball 1, and has a magnitude of 5m. The final momentum has contributions from both balls. Relating the two,
Implying that
| (m1f+m2f)2 | = | 25 | |
| m1f2 + m2f2 +2m1fm2f | = | 25 |
But we know from our kinetic energy equation that 25 = v1f2 + v2f2 . Substituting this in we find that


 payment page
payment page



