Please wait while we process your payment
If you don't see it, please check your spam folder. Sometimes it can end up there.
If you don't see it, please check your spam folder. Sometimes it can end up there.
Please wait while we process your payment
Get instant, ad-free access to our grade-boosting study tools with a 7-day free trial!
Learn more



This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!

Annual
2-49 accounts
$22.49/year + tax
50-99 accounts
$20.99/year + tax
Select Quantity
Price per seat
$29.99 $--.--
Subtotal
$-.--
Want 100 or more? Request a customized plan
You could save over 50%
by choosing an Annual Plan!

SAVE OVER 50%
compared to the monthly price!
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
$22.49/month + tax
Save 25%
on 2-49 accounts
$20.99/month + tax
Save 30%
on 50-99 accounts
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!
You will only be charged after the completion of the 7-day free trial.
If you cancel your account before the free trial is over, you will not be charged.
You will only be charged after the completion of the 7-day free trial. If you cancel your account before the free trial is over, you will not be charged.
Order Summary
Annual
7-day Free Trial
SparkNotes PLUS
$29.99 / year
Annual
Quantity
51
PLUS Group Discount
$29.99 $29.99 / seat
Tax
$0.00
SPARK25
-$1.25
25% Off
Total billed on Nov 7, 2024 after 7-day free trail
$29.99
Total billed
$0.00
Due Today
$0.00
Promo code
This is not a valid promo code
Card Details
By placing your order you agree to our terms of service and privacy policy.
By saving your payment information you allow SparkNotes to charge you for future payments in accordance with their terms.
Powered by stripe
Legal
Google pay.......



Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Your PLUS subscription has expired
Please wait while we process your payment
Please wait while we process your payment

Collisions in One Dimension
The most simple case of a collision is a one-dimensional, or head-on collision. Because of the conservation of energy and momentum we are able to predict a great deal about these collisions, and to calculate relevant quantities after the collision occurs. Before we do so, however, we must define exactly what is meant by a collision.
We all know, somewhat intuitively, the common meaning of a collision: two things hitting each other. Whether the objects are two billiard balls, two particles, or two cars, this common definition applies. The definition used in physics, however, is something more precise. In physics, a collision has two aspects:
A typical collision problem involves two particles with known initial velocities colliding; we are required to calculate the final velocity of each object. If we knew the forces acting during the collision this would be easy. Usually, however, we do not, and are forced to look for other methods of solving the problem. For instance, two balls of the same masses and initial velocities upon hitting a wall bounce back with different velocities according to the "bounciness" or elasticity of the ball. We will examine the cases in which collision problems are soluble, and make some general statements about collisions.
A special category of collisions is called elastic collisions. Formally, an elastic condition is one in which kinetic energy is conserved. This may be difficult to grasp conceptually, so consider the following test: drop a ball from a certain height. If it hits the floor and returns to its original height, the collision between the ball and the floor is elastic. Otherwise it is inelastic. Collisions between pool balls are generally elastic; car crashes are generally inelastic.
Why are these collisions special? We know with all collisions that momentum is conserved. If two particles collide we can use the following equation:
| m1v1o + m2v2o = m1v1f + m2v2f |
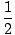 m1v1o2 + m1v1o2 + 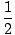 m2v2o2 = m2v2o2 = 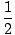 m1v1f2 + m1v1f2 + 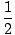 m2v2f2 m2v2f2 |
So what if energy is not conserved? Our knowledge of such situations is more limited, since we no longer know what the kinetic energy is after the collision. However, even though kinetic energy is not conserved, momentum will always be conserved. This allows us to make some statements about inelastic collisions. Specifically, if we are given the masses of the particles, both initial velocities and one final velocity we can calculate the final velocity of the last particle through the familiar equation:
| m1v1o + m2v2o = m1v1f + m2v2f |
Please wait while we process your payment





