The Wave Equations
A traveling wave is a self-propagating disturbance of a medium that moves through space transporting
energy and momentum. Examples include waves on strings, waves in the ocean, and sound waves. Waves
also have the property that they are a continuous entity that exists over the an entire region of space; this
distinguishes them from particles, which are localized objects. There are two basic types of waves:
longitudinal waves, in which the medium is displaced in the direction of propagation (sound
waves are of this type), and transverse waves, in which the medium is displaced in a direction
perpendicular to the direction of propagation (electromagnetic waves and waves on a string are examples).
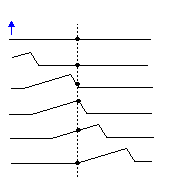
It is important to remember that the individual 'bits' of the medium do not advance with the wave; they
oscillate about an equilibrium position. Consider, for instance, a wave on a string: if the string is given a
flick upwards from one end, any particular bit of string will be observed to move upwards and downwards,
but not in the direction of the wave (see ).
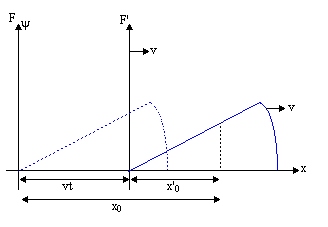
| ψ(x, t) = f (x - vt) |
This is called the wavefunction . What this means is to generate a traveling wave, all we have to do is decide on a shape (pick f (x)) then substitute x - vt for x in f (x). Even though the displacement of the medium may occur in a different direction to the motion of the wave, the wave moves along a line, so this is called a one-dimensional wave.
We now want to find a partial differential equation to define all waves. Since ψ(x, t) = f (x') we can take the partial derivative with respect to x to find:
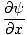 = = 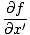 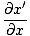 = = 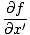 |
and the partial derivative with respect to t:
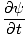 = = 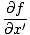 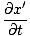 = ±v = ±v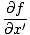 |
since x' = x±vt. Then:
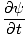 = ±v = ±v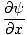 |
Then taking second derivatives with respect to x and t, we have:
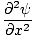 | = 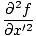 | ||
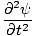 | = ±v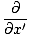 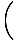 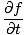 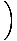 |
But
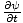 =
= 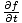 so:
so:
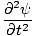 = v2 = v2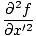 |
So finally we can combine the last equation with our expression for the second derivative with respect to x to find:
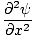 = = 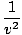 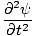 |
This is the second order partial differential equations that governs all waves. It is called the differential wave equation and is very important in many aspects of physics.
Harmonic Waves
One set of extremely important solutions to the differential wave equation are sinusoidal functions. These are called the harmonic waves. One of the reasons they are so important is that it turns out that any wave can be constructed from a sum of harmonic waves--this is the subject of Fourier analysis. The solution in its most general form is given by:
| ψ(x, t) = A sin[k(x - vt)] |
(we could, of course, equally well choose a cosine since the two functions only differ by a phase of Π/2). The argument of the sine is called the phase. A is called the amplitude of the wave and corresponds to the maximum displacement the particles of the medium can experience. The wavelength of a wave (the distance between similar points (eg. peaks) on adjacent cycles) is given by:
λ = 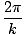 |
k is sometimes called the wave number. The period of the wave (the amount of time taken for a complete cycle to pass a fixed point) is given by
T = 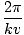 = = 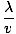 |
As usual, the frequency, ν, is just the inverse of this, ν = 1/T = v/λ. If a complete cycle comprises 2Π radians, then the number of radians of a cycle that pass a fixed point per interval of time is given by the angular frequency, σ = 2Π/T = 2Πν. Thus the harmonic wave may also be expressed as: ψ(x, t) = A sin(kx - σt). A fixed point on the wave, such as a particular peak, moves along with the wave at the phase velocity v = σ/k.
The Principle of Superposition
One property of the differential wave equation is that it is linear. This means that if you find two solutions ψ1 and ψ2 that both satisfy the equation, then (ψ1 + ψ2) must also be a solution. This is easily proved. We have:
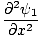 | = 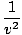 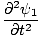 | ||
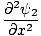 | = 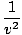 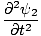 |
Adding these gives:
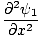 + + 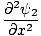 | = | 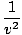 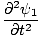 + + 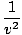 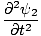 | |
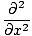 (ψ1 + ψ2) (ψ1 + ψ2) | = | 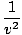 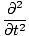 (ψ1 + ψ2) (ψ1 + ψ2) |
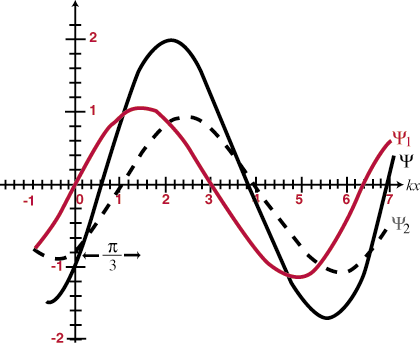
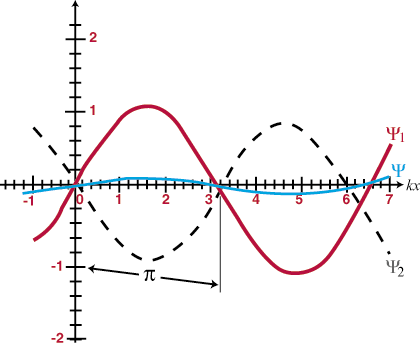
This means that when two waves overlap in space, they will simply 'add up;' the resulting disturbance at each point of overlap will be the algebraic sum of the individual waves at that location. Moreover, once the waves pass each other, they will continue on as if neither had ever encountered the other. This is called the principle of superposition. When waves add up to form a greater total amplitude than either of the constituent waves it is called constructive interference, and when the amplitudes partially or wholly cancel each other out it is called destructive interference. Identical waves that overlap completely are said to be in-phase and will constructively interfere at all points, with an amplitude double that of either constituent wave. Otherwise identical waves (that is they have the same frequency and amplitude) that differ in phase by exactly 180o (Π radians) are said to be out-of-phase, and will destructively interfere at all points. Some examples are illustrated in and . The principle of superposition will come to be of vital importance in the rest of our study of optics.