Now that we have established the theory and equations behind harmonic motion, we will examine various physical situations in which objects move in simple harmonic motion. Previously, we worked with a mass-spring system, and will examine other harmonic oscillators in a similar manner. Finally, after establishing these applications, we can examine the similarity between simple harmonic motion and uniform circular motion.
The Torsional Oscillator
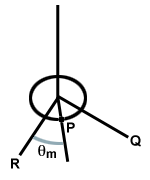
Consider a circular disk suspended from a wire fixed to a ceiling. If the disk
is rotated, the wire will twist. When the disk is released, the twisted wire
exerts a restoring
force
on
the disk, causing it to rotate past its equilibrium point, twisting the wire the
other direction, as shown below. This system is called a torsional
oscillator.
| τ = - κθ |
where κ is a proportionality constant, a property of the wire. Note the similarity to our spring equation F = - kx. Since τ = Iα for any rotational motion we can state that
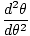
| θ = θmcos(σt) |
where θm is defined as the maximum angular displacement and σ is the angular frequency given by σ =
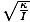 . Note: It is important not to confuse
angular frequency and angular velocity. σ in this case refers to the
angular frequency of the oscillation, and cannot be used for angular velocity.
. Note: It is important not to confuse
angular frequency and angular velocity. σ in this case refers to the
angular frequency of the oscillation, and cannot be used for angular velocity.
From our expression for angular frequency we can derive that
T = 2Π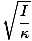 |
This equation for the period of a torsional oscillator has a significant experimental use. Suppose a body of unknown moment of inertia is placed on a wire of known constant κ. The period of oscillation can be measured, and the moment of inertia of the body can be determined experimentally. This is quite useful, as the rotational inertia of most bodies cannot be easily determined using the traditional calculus-based method.
From our examination of the torsional oscillator we have derived that its motion is simple harmonic. This oscillator can almost be seen as the rotational analogue of the mass-spring system: just as with the mass-spring we substituted θ for x, I for m and κ for k. Not all simple harmonic oscillators have such close correlation.
The Pendulum
Another common oscillation is that of the simple pendulum. The classic pendulum consists of a particle suspended from a light cord. When the particle is pulled to one side and released, it swings back past the equilibrium point and oscillates between two maximum angular displacements. It is clear that the motion is periodic--we want to see if it is simple harmonic.
We do so by drawing a free body diagram and examining the forces on the pendulum
at any given time.

| F = - mg sinθ |
In this case the restoring force is not proportional to the angular displacement θ, but is rather proportional to the sine of the angular displacement, sinθ. Strictly speaking, then, the pendulum does not engage in simple harmonic motion. However, most pendulums function at very small angles. If the angle is small we may make the approximation sinθ
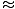 θ. With this approximation we can rewrite our force
expression:
θ. With this approximation we can rewrite our force
expression:
F = - mg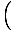 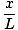 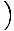 = - = - 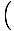 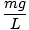 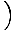 x x |
Thus we have an equation in the same form as our mass-spring equation; in this case k =
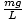 . We can skip the calculus and simply state the period
of the pendulum:
. We can skip the calculus and simply state the period
of the pendulum:
pendulum
T = 2Π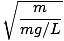 = 2Π = 2Π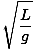 |
Note that the period, and thus the frequency, of the pendulum is independent of the mass of the particle on the cord. It only depends on the length of the pendulum and the gravitational constant. Keep in mind, also, that this is only an approximation. If the angle exceeds more than fifteen degrees or so, the approximation breaks down.


 payment page
payment page



