Longitudinal Doppler Effect
There are two distinct results for the Doppler effect is Special Relativity. The longitudinal Doppler effect considers the simpler case of a source moving directly towards you or away from you along a straight line. The transverse Doppler effect, on the other hand, considers what is observed when the observer is displaced in a direction perpendicular to the direction of the motion. We will take the simpler case first. In this section we must be careful to distinguish, as we have not done elsewhere, between the time an event occurs in the observer's frame and the time when the observer sees it occur; that is, we have to calculate the time it takes for the light to travel from the event to the eye of the observer.
Consider a source (say a laser beam mounted on a train) coming directly towards you. The light of the laser it its own frame is f' and the train is traveling with speed v. The overall effect of the longitudinal Doppler shift is due to both the time dilation that occurs between the frames and the normal Doppler effect due to the motion of the source. For a source moving towards you, its motion compresses the wavelength of the light, increasing the frequency that is observed. If the frequency is f' in the source's frame, then the time between the emission of 'peaks' in the light waves is Δt' = 1/f'. Due to time dilation the time between emission in the observers frame is then: Δt = γΔt'. One peak travels a distance cΔt = cγΔt' before the next peak is emitted. Similarly, in this time between peaks the source travels vΔt = vγΔt'. Hence the distance between peaks in the observer's frame is cΔt - vΔt = (c - v)γΔt', where the minus sign arises because the second peak 'catches up' with the first due to the motion of the source, decreasing the distance between peaks. This holds for all adjacent peaks. The time ΔT between the arrival of peaks at the observer's eye is the distance between peaks divided by their speed, c, thus:
ΔT = 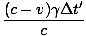 = = 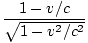 Δt' = Δt' = 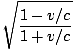 Δt' Δt' |
The observed frequency is just f = 1/ΔT:
f = 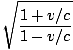 f' f' |
Note that if the source is moving away from the observer, v/c is negative and thus f < f'. For the source approaching the observer, f > f'. This result is qualitatively the same as for the normal (non-relativistic) Doppler effect.
Transverse Doppler Effect
Consider the x - y plane with an observer at rest at the origin. A straight train track traverses the line y = y0. A train with a laser mounted on it emits light with frequency f'. Consider :
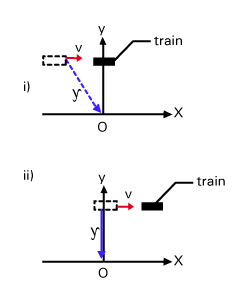
In the first case, let us consider things from the frame of the train. An observer on the train, O' sees the
observer at the origin O moving past to the left with speed v. The light in question hits O just as he
crosses the y'-axis in O'. Time dilation
tells us that O's clock ticks slowly such that
Δt' = γΔt. To say the opposite (Δt = γΔt') is not true of
the time at which O sees the light arrive. This is because for Δt = γΔt' to
hold we need Δx' = 0; this is true of the emission of the light, but since O is moving in the frame of
the train, O does not receive adjacent light pulses in the same place, hence Δx'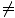 0. Thus it is
true that the frequency of the light is lower is the frame of O than in the frame of O', but because of the
relative motion of the source and observer O observes the frequency as being higher, as we shall see. If
we want to analyze the situation from the point of view of O, we have to take longitudinal effects into
account; by using O' we have avoided this complication. In the frame of the train, then, the observer at
the origin gets hit by a 'peak' every Δt' = 1/f' seconds (Here we make the assumption that the train is
close to the y'-axis and thus that the distance between the train and the source is constant at y0 for the
time it takes the light to reach the observer--in this way we eliminate any longitudinal effects). The
observer at rest then gets hit by a 'peak' every ΔT seconds, where:
0. Thus it is
true that the frequency of the light is lower is the frame of O than in the frame of O', but because of the
relative motion of the source and observer O observes the frequency as being higher, as we shall see. If
we want to analyze the situation from the point of view of O, we have to take longitudinal effects into
account; by using O' we have avoided this complication. In the frame of the train, then, the observer at
the origin gets hit by a 'peak' every Δt' = 1/f' seconds (Here we make the assumption that the train is
close to the y'-axis and thus that the distance between the train and the source is constant at y0 for the
time it takes the light to reach the observer--in this way we eliminate any longitudinal effects). The
observer at rest then gets hit by a 'peak' every ΔT seconds, where:
ΔT = Δt'/γ =  âá’ âá’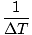 = f = γf' = = f = γf' = 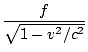 |
Thus, like the longitudinal Doppler effect, the frequency observed at the origin (for someone at rest) is greater than the emitted frequency.
In the second case we can work in the frame of O without complication. O sees the clock of O' run slowly (since O' is moving relative to O), and thus Δt = γΔt'. Here the observed frequency is:
f = 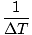 = = 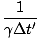 = = 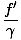 = f' = f'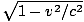 |
In this case the observed frequency (for the observer at rest at the origin) is less than the emitted frequency by a factor γ.


 payment page
payment page



